题目内容
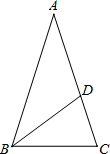 如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
考点:相似三角形的判定与性质,等腰三角形的性质,黄金分割,解直角三角形
专题:计算题
分析:(1)由等腰三角形ABC中,利用顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;
(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;
(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.
(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;
(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.
解答:解:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∵∠CBD=∠A=36°,∠C=∠C,
∴△ABC∽△BCD;
(2)∵∠A=∠ABD=36°,
∴AD=BD,
∵BD=BC,
∴AD=BD=BC=1,
设CD=x,则有AB=AC=x+1,
∵△ABC∽△BCD,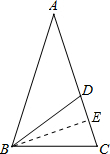
∴
=
,即
=
,
整理得:x2+x-1=0,
解得:x1=
,x2=
(负值,舍去),
则x=
;
(3)过B作BE⊥AC,交AC于点E,
∵BD=BC,
∴E为CD中点,即DE=CE=
,
在Rt△ABE中,cosA=cos36°=
=
=
,
在Rt△BCE中,cosC=cos72°=
=
=
,
则cos36°-cos72°=
-
=
.
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∵∠CBD=∠A=36°,∠C=∠C,
∴△ABC∽△BCD;
(2)∵∠A=∠ABD=36°,
∴AD=BD,
∵BD=BC,
∴AD=BD=BC=1,
设CD=x,则有AB=AC=x+1,
∵△ABC∽△BCD,

∴
| AB |
| BD |
| BC |
| CD |
| x+1 |
| 1 |
| 1 |
| x |
整理得:x2+x-1=0,
解得:x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
则x=
-1+
| ||
| 2 |
(3)过B作BE⊥AC,交AC于点E,
∵BD=BC,
∴E为CD中点,即DE=CE=
-1+
| ||
| 4 |
在Rt△ABE中,cosA=cos36°=
| AE |
| AB |
1+
| ||||
|
| ||
| 4 |
在Rt△BCE中,cosC=cos72°=
| EC |
| BC |
| ||||
| 1 |
-1+
| ||
| 4 |
则cos36°-cos72°=
| ||
| 4 |
-1+
| ||
| 4 |
| 1 |
| 2 |
点评:此题考查了相似三角形的判定与性质,锐角三角函数定义,以及一元二次方程的解法,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
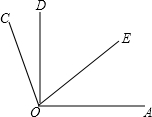 如图,OE为∠AOD的平分线,∠COD=
如图,OE为∠AOD的平分线,∠COD= 如图,用火柴棍连续搭建三角形和正方形,公共边只用一根火柴棍.如果搭建三角形和正方形共用了77根火柴棍,并且三角形的个数比正方形的个数少5个,那么一共能连续搭建三角形、正方形各多少个?
如图,用火柴棍连续搭建三角形和正方形,公共边只用一根火柴棍.如果搭建三角形和正方形共用了77根火柴棍,并且三角形的个数比正方形的个数少5个,那么一共能连续搭建三角形、正方形各多少个? 如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=26°,则∠AOC=
如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=26°,则∠AOC=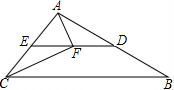 如图,在△ABC中,∠ACB=58°,D,E分别是AB,AC中点.点F在线段DE上,且AF⊥CF,则∠FAE=
如图,在△ABC中,∠ACB=58°,D,E分别是AB,AC中点.点F在线段DE上,且AF⊥CF,则∠FAE= 如图,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2014厘米后停下,则这只蚂蚁停在
如图,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2014厘米后停下,则这只蚂蚁停在