题目内容
 如图,在梯形ABCD中,AD∥BC,BD=CD,AD=1,BC=8,∠BDC=90°,则AB的长为
如图,在梯形ABCD中,AD∥BC,BD=CD,AD=1,BC=8,∠BDC=90°,则AB的长为考点:梯形
专题:
分析:作辅助线,先求出DM的长,再求出BN的长,在RT△ANB中运用勾股定理求出AB即可.
解答:
解:如图,作DM⊥BC交BC于点M,作AN⊥BC交BC于点N,
∵BD=CD,BC=8,∠BDC=90°,
∴DM=MC=BM=4,
∵AD∥BC,AD=1,
∴四边形ANMD是矩形,
∴NM=1,AN=DM=4,
∴BN=8-4-1=3,
∴AB=
=
=5,
故答案为:5.

解:如图,作DM⊥BC交BC于点M,作AN⊥BC交BC于点N,
∵BD=CD,BC=8,∠BDC=90°,
∴DM=MC=BM=4,
∵AD∥BC,AD=1,
∴四边形ANMD是矩形,
∴NM=1,AN=DM=4,
∴BN=8-4-1=3,
∴AB=
| AN2+BN2 |
| 32+42 |
故答案为:5.
点评:本题主要考查了梯形及直角三角形的知识,解题的关键是求出DM的长.

练习册系列答案
相关题目
在△ABC和△A′B′C′中A′B′=AB,∠B=∠B′,补充条件后仍不一定能保证△A′B′C′≌△ABC,则补充的条件是( )
| A、A′C′=AC |
| B、B′C′=BC |
| C、∠A′=∠A |
| D、∠C′=∠C |
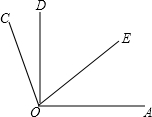 如图,OE为∠AOD的平分线,∠COD=
如图,OE为∠AOD的平分线,∠COD=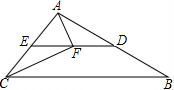 如图,在△ABC中,∠ACB=58°,D,E分别是AB,AC中点.点F在线段DE上,且AF⊥CF,则∠FAE=
如图,在△ABC中,∠ACB=58°,D,E分别是AB,AC中点.点F在线段DE上,且AF⊥CF,则∠FAE= 服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图.
服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图. 如图,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2014厘米后停下,则这只蚂蚁停在
如图,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2014厘米后停下,则这只蚂蚁停在