题目内容
14.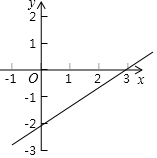 如图,是一次函数y=kx+b的图象,下面哪个点在图象上( )
如图,是一次函数y=kx+b的图象,下面哪个点在图象上( )| A. | (-3,-4) | B. | (-1,-3) | C. | (2,-1) | D. | (6,1) |
分析 观察图形找出直线与坐标轴的交点坐标,利用待定系数法即可求出一次函数解析式,再将四个选项给出的点的横坐标代入一次函数解析式中求出y值,对照后即可得出结论.
解答 解:将(0,-2)、(3,0)代入y=kx+b,
$\left\{\begin{array}{l}{b=-2}\\{3k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=-2}\end{array}\right.$,
∴该一次函数解析式为y=$\frac{2}{3}$x-2.
A、∵当x=-3时,y=$\frac{2}{3}$×(-3)-2=-4,
∴A选项给出的点在一次函数y=$\frac{2}{3}$x-2的图象上;
B、∵当x=-1时,y=$\frac{2}{3}$×(-1)-2=-$\frac{8}{3}$,
∴B选项给出的点不在一次函数y=$\frac{2}{3}$x-2的图象上;
C、∵当x=2时,y=$\frac{2}{3}$×2-2=-$\frac{2}{3}$,
∴C选项给出的点不在一次函数y=$\frac{2}{3}$x-2的图象上;
D、∵当x=6时,y=$\frac{2}{3}$×6-2=2,
∴D选项给出的点不在一次函数y=$\frac{2}{3}$x-2的图象上.
故选A.
点评 本题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,根据点的坐标利用待定系数法求出一次函数解析式是解题的关键.

练习册系列答案
相关题目
2.如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程2-(x-a)(x-b)=0的两根,且a<b,则a、b、m、n的大小关系是( )
| A. | a<m<n<b | B. | m<a<b<n | C. | a<m<b<n | D. | m<a<n<b |
3.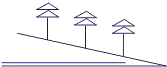 在山坡上植树,要求两棵树间的水平距离是m,测得斜坡的倾斜角为α,则斜坡上相邻两棵树的坡面距离是( )
在山坡上植树,要求两棵树间的水平距离是m,测得斜坡的倾斜角为α,则斜坡上相邻两棵树的坡面距离是( )
 在山坡上植树,要求两棵树间的水平距离是m,测得斜坡的倾斜角为α,则斜坡上相邻两棵树的坡面距离是( )
在山坡上植树,要求两棵树间的水平距离是m,测得斜坡的倾斜角为α,则斜坡上相邻两棵树的坡面距离是( )| A. | $\frac{m}{sinα}$ | B. | $\frac{m}{cosα}$ | C. | m•tanα | D. | m•cosα |
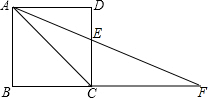 已知,点F在正方形ABCD的边BC的延长线上,且AC=CF,求∠F及∠AEC的度数.
已知,点F在正方形ABCD的边BC的延长线上,且AC=CF,求∠F及∠AEC的度数.
 如图,若要得到AD∥EF,需要添加的条件是(只填一个条件)∠2=∠3.
如图,若要得到AD∥EF,需要添加的条件是(只填一个条件)∠2=∠3.
 如图所示的几何体是由7个相同的小正方体搭成的,请画出它的左视图和俯视图.
如图所示的几何体是由7个相同的小正方体搭成的,请画出它的左视图和俯视图.