题目内容
3．
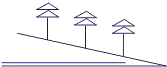在山坡上植树，要求两棵树间的水平距离是m，测得斜坡的倾斜角为α，则斜坡上相邻两棵树的坡面距离是（ ）| A． | $\frac{m}{sinα}$ | B． | $\frac{m}{cosα}$ | C． | m•tanα | D． | m•cosα |
分析 根据坡角的定义、余弦的概念列式计算即可．
解答 解：
作AB⊥BC于B，
cosα=$\frac{AB}{AC}$，
∴斜坡上相邻两棵树的坡面距离AB=$\frac{AC}{cosα}$=$\frac{m}{cosα}$，
故选：B．
点评 本题考查的是解直角三角形的应用-仰角俯角问题，掌握坡角的概念、熟记锐角三角函数的定义是解题的关键．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
作图题
14．
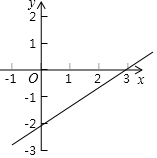如图，是一次函数y=kx+b的图象，下面哪个点在图象上（ ）
如图，是一次函数y=kx+b的图象，下面哪个点在图象上（ ）| A． | （-3，-4） | B． | （-1，-3） | C． | （2，-1） | D． | （6，1） |
如图，在平面直角坐标系中，已知A（9，0），B（0，6），⊙M经过原点O及点A、B．
如图是一个正方体的平面展开图，试问：将其折叠成正方体后，红、黄、绿的对面分别是什么面？
8．由于x轴上的点的纵坐标为零，y轴上的点的横坐标为零，因此在求直线y=kx+b与y轴、x轴的交点坐标时，只需令x=0和y=0，即可分别求出直线y=kx+b（k≠0）与y轴，x轴交点的纵坐标，横坐标．
15．下列基本几何体中，三视图都是相同图形的是（ ）
| A． |  圆柱 | B． |  三棱柱 | C． |  球 | D． |  长方体 |