题目内容
8.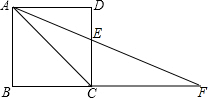 已知,点F在正方形ABCD的边BC的延长线上,且AC=CF,求∠F及∠AEC的度数.
已知,点F在正方形ABCD的边BC的延长线上,且AC=CF,求∠F及∠AEC的度数.
分析 根据正方形的对角线平分一组对角求出∠ACB=45°,根据等边对等角可得∠F=∠CAF,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACB=∠F+∠CAF,然后求解即可;根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AEC=∠F+∠ECF.
解答 解:∵四边形ABCD是正方形,
∴∠ACB=45°,
∵AC=CF,
∴∠F=∠CAF,
由三角形的外角性质得,∠ACB=∠F+∠CAF,
所以,2∠F=45°,
解得∠F=22.5°;
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠ECF=90°,
由三角形的外角性质得∠AEC=∠F+∠ECF=22.5°+90°=112.5°.
点评 本题考查了正方形的性质,等边对等角的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
14.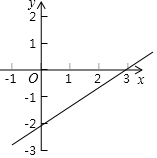 如图,是一次函数y=kx+b的图象,下面哪个点在图象上( )
如图,是一次函数y=kx+b的图象,下面哪个点在图象上( )
 如图,是一次函数y=kx+b的图象,下面哪个点在图象上( )
如图,是一次函数y=kx+b的图象,下面哪个点在图象上( )| A. | (-3,-4) | B. | (-1,-3) | C. | (2,-1) | D. | (6,1) |
 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(9,0),(0,4),点D的坐标为(5,0),点P沿矩形的边C-B-A-O-C运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(3,4)、(2,4)、(8,4)、(9,3).
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(9,0),(0,4),点D的坐标为(5,0),点P沿矩形的边C-B-A-O-C运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(3,4)、(2,4)、(8,4)、(9,3).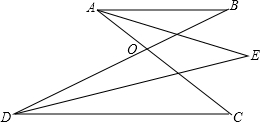 如图,AB∥CD,AC、BD交于点O,∠A、∠D的角平分线交于点E,已知∠E=50°,求∠AOB的度数.
如图,AB∥CD,AC、BD交于点O,∠A、∠D的角平分线交于点E,已知∠E=50°,求∠AOB的度数. 如图,已知:AB∥CD,求证:∠AEC=∠A+∠C.
如图,已知:AB∥CD,求证:∠AEC=∠A+∠C.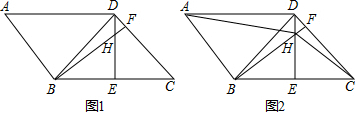
 作图题
作图题