题目内容
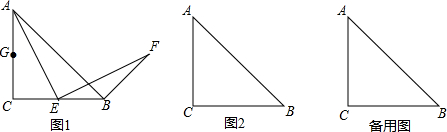
1.【问题】在△ABC中,AC=BC,∠ACB=90°,点E在直线BC上(B,C除外),分别经过点E和点B作AE和AB的垂线,两条垂线交于点F,研究AE和EF的数量关系.
【探究发现】
某数学兴趣小组在探究AE,EF的关系时,运用“从特殊到一般”的数学思想,他们发现当点E是BC的中点时,只需要取AC边的中点G(如图1),通过推理证明就可以得到AE和EF的数量关系,请你按照这种思路直接写出AE和EF的数量关系;
【数学思考】
那么当点E是直线BC上(B,C除外)(其它条件不变),上面得到的结论是否仍然成立呢?请你从“点E在线段BC上”;“点E在线段BC的延长线”;“点E在线段BC的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论;
【拓展应用】
当点E在线段CB的延长线上时,若BE=nBC(0<n<1),请直接写出S△ABC:S△AEF的值.
分析 【数学思考】在AC上截取CG=CE,连接GE,证明△AGE≌△EBF,得到答案;
【拓展应用】设BC=1,则BE=n,根据勾股定理求出AE2,根据等腰直角三角形的面积公式求解即可.
解答 解:
【探究发现】:相等;
【数学思考】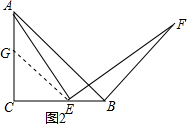
证明:如图2,点E在线段BC上,
在AC上截取CG=CE,连接GE,
∵∠ACB=90°,
∴∠CGE=∠CEG=45°,
∵AE⊥EF,AB⊥BF,
∴∠AEF=∠ABF=∠ACB=90°,
∴∠FEB+∠AEF=∠AEB=∠EAC+∠ACB.
∴∠FEB=∠EAC.
∵CA=CB,
∴AG=BE,∠CBA=∠CAB=45°.
∴∠AGE=∠EBF=135°.
在△AGE和△EBF中,
$\left\{\begin{array}{l}{∠AGE=∠EBF}\\{AG=BE}\\{∠EAG=∠FEB}\end{array}\right.$,
∴△AGE≌△EBF.
∴AE=EF;
【拓展应用】
设BC=1,则BE=n,
AE2=AC2+CE2=1+(n+1)2=n2+2n+2,
∵△ABC中,AC=BC,∠ACB=90°,
∴△ABC的面积=$\frac{1}{2}$BC2,
∵△AEF是等腰直角三角形,
∴△AEF的面积$\frac{1}{2}$AE2,
∴S△ABC:S△AEF=$\frac{\frac{1}{2}B{C}^{2}}{\frac{1}{2}A{E}^{2}}$=$\frac{1}{{n}^{2}+2n+2}$,
∴S△ABC:S△AEF=1:(n2+2n+2).
点评 本题考查的是相似三角形的知识,掌握全等三角形的判定定理和性质定理、等腰直角三角形的性质、运灵活用“从特殊到一般”的数学思想是解题的关键.

练习册系列答案
相关题目
12.不透明的袋子中装有10个黑球、1个白球,它们除颜色外无其他差别,随机从袋子中摸出一个球,则( )
| A. | 这个球一定是黑球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球可能是白球 | |
| D. | 事先能确定摸到什么颜色的球 |
9.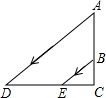 如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
 如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )| A. | 1.5m | B. | 1.6m | C. | 1.86m | D. | 2.16m |
6.下列结论错误的是( )
| A. | 垂直于同一直线的两条直线互相平行 | |
| B. | 两直线平行,同旁内角互补 | |
| C. | 过直线外一点有且只有一条直线与这条直线平行 | |
| D. | 同一平面内,不相交的两条直线叫做平行线 |
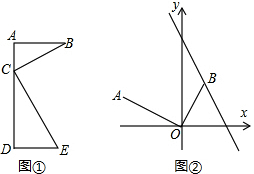 探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):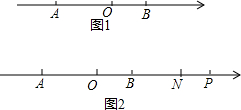 如图1,点A在数轴上对应的数为-3,点B对应的数为2.
如图1,点A在数轴上对应的数为-3,点B对应的数为2.