题目内容
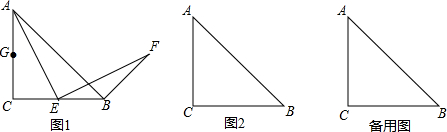
16.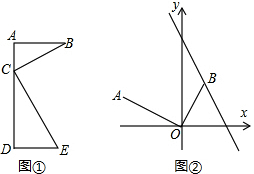 探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):(1)请就图①证明上述“模块”的合理性.已知:∠A=∠D=∠BCE=90°,求证:△ABC∽△DCE;
(2)请直接利用上述“模块”的结论解决下面问题:
如图②,已知点A(-2,1),点B在直线y=-2x+3上运动,若∠AOB=90°,求此时点B的坐标.
分析 (1)根据同角的余角相等和相似三角形的判定定理证明即可;
(2)作AM⊥x轴于M,作BN⊥x轴于N,根据坐标特征求出OM=2,AM=1,根据一次函数图象上点的坐标特征设出点B的坐标,根据相似三角形的性质列出比例式,代入计算即可.
解答 (1)证明:∵∠D=90°,
∴∠DCE+∠E=90°,
∵∠BCE=90°,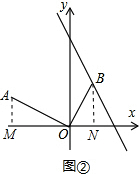
∴∠DCE+∠ACB=90°,
∴∠ACB=∠E,又∠A=∠D=90°,
∴△ABC∽△DCE;
(2)解:如图②,作AM⊥x轴于M,作BN⊥x轴于N,
∵点A(-2,1),
∴OM=2,AM=1,
设点B的坐标为(x,-2x+3),
由(1)得,△AOM∽△OBN,
∴$\frac{AM}{ON}$=$\frac{OM}{BN}$,即$\frac{1}{x}$=$\frac{2}{-2x+3}$,
解得,x=$\frac{3}{4}$,
则-2x+3=$\frac{3}{2}$,
则点B的坐标为($\frac{3}{4}$,$\frac{3}{2}$).
点评 本题考查的是相似三角形的判定和性质、一次函数图象上点的坐标特征,掌握相似三角形的判定定理和性质定理、理解一次函数图象上点的坐标特征是解题的关键.

练习册系列答案
相关题目
4.下列各式计算正确的是( )
| A. | a6÷a3=a2 | B. | (a3)2=a5 | C. | $\sqrt{4}$=±2 | D. | $\root{3}{-8}$=-2 |
1. 如图,将?ABCD折叠,使顶点D落在AB边上的M处,折痕为AN.则下列结论中错误的是( )
如图,将?ABCD折叠,使顶点D落在AB边上的M处,折痕为AN.则下列结论中错误的是( )
 如图,将?ABCD折叠,使顶点D落在AB边上的M处,折痕为AN.则下列结论中错误的是( )
如图,将?ABCD折叠,使顶点D落在AB边上的M处,折痕为AN.则下列结论中错误的是( )| A. | MN∥BC | B. | AD∥MN | C. | MN=AM | D. | AN=AM |
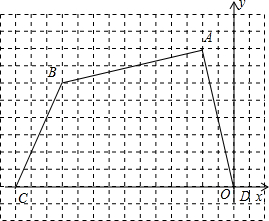 如图,四边形ABCD各个顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).
如图,四边形ABCD各个顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).