题目内容
5.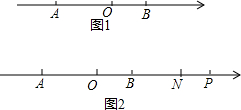 如图1,点A在数轴上对应的数为-3,点B对应的数为2.
如图1,点A在数轴上对应的数为-3,点B对应的数为2.(1)求线段AB的长;
(2)在数轴上是否存在点P,使PA+PB=8?若存在,求出点P对应的数;若不存在,说明理由;
(3)如图,若P点是B点右侧一点,PA的中点为M,N为PB的三等分点且靠近于P点,当P在B的右侧运动时,求PM-$\frac{3}{4}$BN的值.
分析 (1)由数轴上的两点距离公式直接求得;
(2)设出点P代表的数,列式求解即可,要分类讨论;
(3)设P点所表示的数为n,就有PA=n+3,PB=n-2,根据条件就可以表示出PM=$\frac{n+3}{2}$,BN=$\frac{2}{3}$×(n-2),再分别代入PM-$\frac{3}{4}$BN求出其值即可.
解答 解:(1)线段AB的长=2-(-3)=5;
(2)设点P表示的数为x,当点P在点A左侧,根据PA+PB=8,
∴-3-x+2-x=8,解得:x=-4.5,
当点P在点A左侧,根据PA+PB=8,
∴x-(-3)+x-2=8,解得:x=3.5,
当点P在线段AB上时,可求PA+PB=5,与题意不符,
∴点P对应的数为:-4.5和3.5;
(3)设P点所表示的数为n,
∴PA=n+3,PB=n-2.
∵PA的中点为M,
∴PM=$\frac{1}{2}$PA=$\frac{n+3}{2}$.
N为PB的三等分点且靠近于P点,
∴BN=$\frac{2}{3}$PB=$\frac{2}{3}$×(n-2).
∴PM-$\frac{3}{4}$BN=$\frac{n+3}{2}$-$\frac{3}{4}$×$\frac{2}{3}$×(n-2)=$\frac{5}{2}$.
点评 本题主要考查一元一次方程的运用,数轴的运用,数轴上任意两点间的距离公式的运用,对于告诉距离求点时注意分类讨论是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
18.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )

| A. | 2条 | B. | 3条 | C. | 4条 | D. | 5条 |
15.下列式子可以用平方差公式计算的是( )
| A. | (x-4)(4-x) | B. | (-a-3)(3-a) | C. | (a+b)(-a-b) | D. | (2y-4)(-4+2y) |


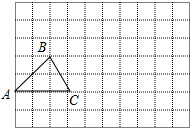 在如图所示的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上.
在如图所示的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上.