题目内容
9.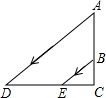 如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )| A. | 1.5m | B. | 1.6m | C. | 1.86m | D. | 2.16m |
分析 由于光线是平行的,因此BE和AD平行,可判定两个三角形相似,根据三角形相似的性质,对应线段成比例,列出等式求解即可得出AB.
解答 解:∵BE∥AD,
∴△BCE∽△ACD,
∴$\frac{CB}{CA}=\frac{CE}{CD}$即$\frac{BC}{AB+BC}$=$\frac{EC}{EC+DE}$
且BC=1,DE=1.8,EC=1.2
∴$\frac{1}{AB+1}$=$\frac{1.2}{1.2+1.8}$
∴1.2AB=1.8,
∴AB=1.5m.
故选:A.
点评 本题主要考查平行投影,只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出窗户的高.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
4.下列各式计算正确的是( )
| A. | a6÷a3=a2 | B. | (a3)2=a5 | C. | $\sqrt{4}$=±2 | D. | $\root{3}{-8}$=-2 |
18.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )

| A. | 2条 | B. | 3条 | C. | 4条 | D. | 5条 |
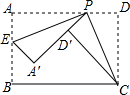 如图,有一张矩形纸片ABCD,AB=3,BC=4,点P是AD边上任意一点(与点A,D不重合),现将△PCD沿PC翻折,得到△PCD′,再在AB边上选取适当的点E,将△PAE沿PE翻折,得到△PA′E,并使直线PD′,PA重合,线段AE的最大值为$\frac{4}{3}$.
如图,有一张矩形纸片ABCD,AB=3,BC=4,点P是AD边上任意一点(与点A,D不重合),现将△PCD沿PC翻折,得到△PCD′,再在AB边上选取适当的点E,将△PAE沿PE翻折,得到△PA′E,并使直线PD′,PA重合,线段AE的最大值为$\frac{4}{3}$.
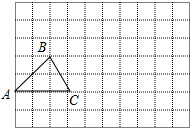 在如图所示的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上.
在如图所示的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上.