题目内容
下列说法不正确的是( )
| A、等腰三角形两腰上的中线相等 |
| B、等腰三角形两底角平分线相等 |
| C、等腰三角形的高,中线,角平分线互相重合 |
| D、等边三角形的高,中线,角平分线互相重合 |
考点:等腰三角形的性质
专题:
分析:根据条件证明三角形全等可判定A、B正确,结合等边三角形的性质可判定D正确,根据三线合一性质的条件可知C不正确,可得出答案.
解答:解:如图1,在△ABC中,AB=AC,BD、CE分别是AC、AB边上的中线,
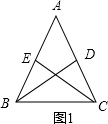
则可知CD=BE,且∠DCB=∠EBC,
在△CDB和△BEC中
∴△CDB≌△BEC(SAS),
∴BD=CE,
故A正确;
如图2,在△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,
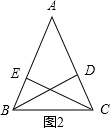
则可知∠DBC=
ABC=
∠ACB=∠ECB,
在△CDB和△BEC中
∴△CDB≌△BEC(ASA),
∴BD=CE,
故B正确;
对等腰三角形有底边上的中线、高和顶角的角平分线互相重合,故C不正确;
由等边三角形的性质可知等边三角形的高,中线,角平分线互相重合,故D正确;
故选C.

则可知CD=BE,且∠DCB=∠EBC,
在△CDB和△BEC中
|
∴△CDB≌△BEC(SAS),
∴BD=CE,
故A正确;
如图2,在△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,

则可知∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
在△CDB和△BEC中
|
∴△CDB≌△BEC(ASA),
∴BD=CE,
故B正确;
对等腰三角形有底边上的中线、高和顶角的角平分线互相重合,故C不正确;
由等边三角形的性质可知等边三角形的高,中线,角平分线互相重合,故D正确;
故选C.
点评:本题主要考查等腰三角形的性质,掌握等腰三角形两腰、两底角相等,底边上的高、中线和顶角的角平分线相互重合是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点E在BD上,AD=AE,AB=AC,∠1=∠2=20°,求∠CEA的度数.
如图,点E在BD上,AD=AE,AB=AC,∠1=∠2=20°,求∠CEA的度数. 一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长.
一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长. 如图,在△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,E是边CA上任意一点,DF⊥DE,交BC于F点.G为EF的中点,连接CG并延长交AB于点H.
如图,在△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,E是边CA上任意一点,DF⊥DE,交BC于F点.G为EF的中点,连接CG并延长交AB于点H. 如图,AD⊥BC,垂足为D,点E在AC上,∠EBC=40°,∠A=30°,求∠BEC的度数.
如图,AD⊥BC,垂足为D,点E在AC上,∠EBC=40°,∠A=30°,求∠BEC的度数.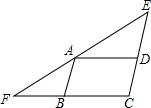 已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.
已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b. 已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC.
已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC. 如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°
如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°