题目内容
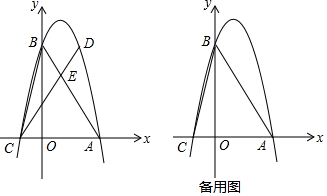
1.如图,抛物线y=-$\frac{4}{3}$x2+bx+c经过A(3,0)、C(-1,0)两点,与y轴交于B点.(1)求抛物线的解析式;
(2)D为第一象限抛物线上的一点,连接CD交AB于E,当CE=2ED时,求点D的坐标;
(3)点P以每秒3个单位长度的速度从点O出发,沿O→B→A匀速运动,同时点Q以每秒1个单位长度的速度从点C出发,沿C→A匀速运动,运动时间为t秒,当一个点到达终点时,另一个点也随之停止运动,是否存在t,使以A、P、Q为顶点的三角形为直角三角形?若存在,直接写出t的值;若不存在,说明理由.
分析 (1)由A、C两点的坐标,利用待定系数法可求得抛物线解析式;
(2)作DF∥AC交AB于F,可证得△ACE∽△FDE,根据相似三角形的性质可求得FD,设出设D(a,-$\frac{4}{3}$a2+$\frac{8}{3}$a+4),则F(a-2,-$\frac{4}{3}$a2+$\frac{8}{3}$a+4),然后求得直线AB的解析式,将点B的坐标代入直线AB的解析式可求得a的值;
(3)先依据题意分析可出可能出现的情况,然后画出相应的图形,最后利用相似三角形的性质求解即可.
解答 解:(1)∵抛物线y=-$\frac{4}{3}$x2+bx+c经过A(3,0)、C(-1,0)两点,
$\left\{\begin{array}{l}{-\frac{3}{4}×{3}^{2}+3b+c=0}\\{-\frac{3}{4}-b+c=0}\end{array}\right.$ 解得$\left\{\begin{array}{l}{b=\frac{8}{3}}\\{c=4}\end{array}\right.$
∴抛物线的解析式是y=-$\frac{4}{3}$x2+$\frac{8}{3}$x+4;
(2)如图1所示:作DF∥AC交AB于F.
设直线AB的解析式为y=kx+b,将点A、B的坐标代入得:$\left\{\begin{array}{l}{b=4}\\{3k+b=0}\end{array}\right.$,
解得:k=-$\frac{4}{3}$,b=4.
∴直线AB的解析式为y=-$\frac{4}{3}$x+4.
∵FD∥AC,
∴△ACE∽△FDE,
∴$\frac{FD}{AC}$=$\frac{DE}{CE}$=$\frac{DE}{2DE}$=$\frac{1}{2}$,
∵AC=4
∴FD=2.
设D(a,-$\frac{4}{3}$a2+$\frac{8}{3}$a+4),则F(a-2,-$\frac{4}{3}$a2+$\frac{8}{3}$a+4),
将点F的坐标代入直线AB的解析式得:-$\frac{4}{3}$a2+$\frac{8}{3}$a+4=-$\frac{4}{3}$(a-2)+4,解得a=1或a=2.
当a=1时,-$\frac{4}{3}$a2+$\frac{8}{3}$a+4=$\frac{16}{3}$,即点D(1,$\frac{16}{3}$).
当a=2时,-$\frac{4}{3}$a2+$\frac{8}{3}$a+4=4,即点D(2,4).
综上所述点D的坐标为(1,$\frac{16}{3}$)或(2,4).
(3)存在.
如图2所示:当∠APA=90°时.
∵∠QPO+∠OPA=90°,∠QPO+∠PQO=90°,
∴∠OPA=∠PQO.
又∵∠POQ=∠POA=90°,
∴△PQO∽△APO.
∴$\frac{PO}{OQ}$=$\frac{OA}{OP}$,即$\frac{3t}{1-2t}$=$\frac{3}{3t}$,解得t=$\frac{-1+\sqrt{13}}{6}$或t=$\frac{-1-\sqrt{13}}{6}$(舍去).
如图3所示:当点Q与点O重合时,△PQP为直角三角形.
∵OC=1,
∴t=1.
如图4所示:当∠PQA=90°时.
由题意可知QA=4-t,AP=9-3t.
∵cos∠BAO=$\frac{OA}{AB}$=$\frac{AQ}{AP}$=$\frac{3}{5}$,
∴$\frac{4-t}{9-3t}$=$\frac{3}{5}$,解得:t=$\frac{7}{4}$.
如图5所示:当∠QPA=90°时.
由题意可知QA=4-t,AP=9-3t.
∵cos∠BAO=$\frac{AP}{QA}$=$\frac{OA}{AB}$═$\frac{3}{5}$,
∴$\frac{9-3t}{4-t}$=$\frac{3}{5}$,解得:t=$\frac{11}{4}$.
综上所述,当t的值为$\frac{-1+\sqrt{13}}{6}$或1或$\frac{7}{4}$或=$\frac{11}{4}$时,△PAQ为直角三角形.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、相似三角形的性质和判定,利用相似三角形的性质表示出点F的坐标是解答问题(2)的关键,根据题意画出符合题意的所有图形是解答问题(3)的关键.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
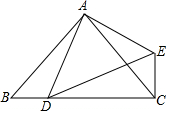 将两块大小不同的等腰直角三角板△ABC与△ADE(其中∠BAC=∠DAE=90°)按如图位置摆放,使点D恰好落在BC边上,求证:BD=CE.
将两块大小不同的等腰直角三角板△ABC与△ADE(其中∠BAC=∠DAE=90°)按如图位置摆放,使点D恰好落在BC边上,求证:BD=CE. 如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).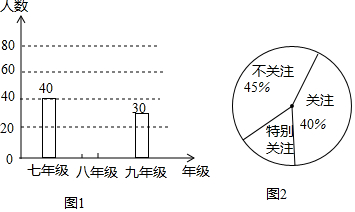
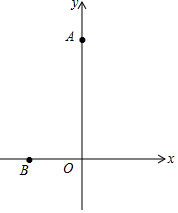 如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.