题目内容
2.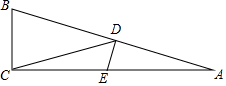 如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E.
如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E.(1)求∠CDE的度数;
(2)求CE:EA.
分析 (1)根据直角三角形斜边上中线得出CD=AD=BD,求出∠DCA=∠A=15°,求出∠BDC=∠A+∠DCA=30°,即可得出答案;
(2)根据线段垂直平分线性质求出BE=AE,求出CE和BE的比,即可得出答案.
解答 解:(1)∵在△ABC中,∠ACB=90°,D是边AB的中点,
∴CD=AD=BD,
∴∠DCA=∠A,
∵∠A=15°,
∴∠DCA=15°,
∴∠BDC=∠A+∠DCA=30°,
∵ED⊥AB,
∴∠EDB=90°,
∴∠CDE=90°-30°=60°;
(2)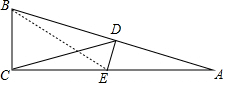
连接BE,
∵D为AB中点,DE⊥AB,
∴BE=AE,
∴∠EBA=∠A=15•,
∴∠BEC=15°+15°=30°,
∴cos30°=$\frac{CE}{BE}$,
∵AE=BE,
∴$\frac{CE}{AE}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了直角三角形斜边上中线性质,线段垂直平分线性质,解直角三角形等知识点,能综合运用知识点进行推理是解此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
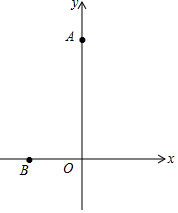 如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
 已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B垂直于x轴的直线交于点D,且CP:PD=1:2
已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B垂直于x轴的直线交于点D,且CP:PD=1:2