题目内容
5.已知点O是坐标系的原点,直线y=-x+4与双曲线y=$\frac{mn}{x}$(mn>0)交于两个不同的点A(m,n)($\frac{5}{2}$<n<4)和B(p,q),AC⊥x轴交于点C,求△ABC的面积S的取值范围.分析 联立直线与双曲线的解析式后,化简可得x2-4x+mn=0,由题意可知n=p,m+n4,过点B作BD⊥x轴于点D,从而求出梯形ABDC的面积以及三角形BCD的面积表达式,即可求出S的表达式.
解答 解:联立$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{mn}{4}}\end{array}\right.$,
化简可得到:x2-4x+mn=0,
由题意可知该方程有两个解,x=m或x=p,
由根与系数的关系可知:mp=mn,
即p=n,
∴B的坐标为(n,m)
∵点A(m,n)在直线y=-x+4,
∴m+n=4,
∵$\frac{5}{2}$<n<4,
∴0<m<$\frac{3}{2}$,
∴A(4-n,n),B(n,4-n),
过点B作BD⊥x轴于点D,
∴CD=n-(4-n)=2n-4,BD=4-n,AC=n,
∴梯形ABDC的面积为:$\frac{(AC+BD)•CD}{2}$=4n-8,
△BCD的面积为:$\frac{1}{2}$CD•BD=-n2+6n-8,
∴△ACB的面积为:S=(4n-8)-(-n2+6n-8)=n2-2n,
对称轴为:n=1,
∴当n=4时,S=42-2×4=8,
当n=$\frac{5}{2}$时,S=($\frac{5}{2}$)2-2×$\frac{5}{2}$=$\frac{5}{4}$
∴S的取值范围:$\frac{5}{4}$<S<8,
点评 本题考查反比例函数的综合问题,解题的关键是求出n=p,从而将A、B的坐标用n表示,本题属于中等题型.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=3,阴影部分面积为15.
如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=3,阴影部分面积为15.
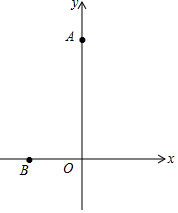 如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.