Question

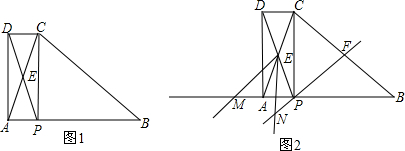
已知点A（a，0）和B（0，b）满足（a-4）²+|b-6|=0，分别过点A、B作x轴、y轴的垂线交于点C，如图，点P从原点出发，以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动．
（1）写出A、B、C三点的坐标；
（2）当点P移动了6秒时，描出此时P点的位置，并写出点P的位置；
（3）连结（2）中B、P两点，将线段BP向下平移h个单位（h＞0），得到B′P′，若B′P′将四边形OACB的周长分成相等的两部分，求h的值．

Answer 1

考点：坐标与图形性质,坐标与图形变化-平移

专题：动点型

分析：（1）根据非负数的性质列式求出a、b的值，然后写出点A、B的坐标，再根据矩形的性质写出点C的坐标；
（2）求出点P运动的路程，然后确定出点P在AC边上并求出AP的值，再写出点P的坐标即可；
（3）根据平移的性质和矩形的性质表示出BB′、CP′、AP′、OB′，然后根据周长的定义列出方程求解即可．

解答：解：（1）由非负数的性质得，a-4=0，b-6=0，
解得a=4，b=6，
所以，A（4，0），B（0，6），C（4，6）；

（2）点P运动的路程=2×6=12，
所以，点P在边AC上，
AP=6+4+6-12=4，
P点的位置如图：P（4，4）；


（3）如图：∵PP′=BB′=h，
∴CP′=h+2，AP′=4-h，OB′=6-h，
∵B′P′将四边形OACB的周长分成相等的两部分，
∴h+4+（h+2）=（6-h）+4+（4-h），
解得h=2．
答：h的值为2．

点评：本题考查了坐标与图形性质，主要利用了几个非负数的和为0时，这几个非负数都为0，矩形的对边相等，平移的性质，比较简单，（3）表示出矩形被分成的两个部分的边长然后列出方程是解题的关键．