题目内容
湖州某公司有甲、乙两个工程队.
(1)两队共同完成一项工程,乙队先单独做1天后,再由两队合做2天完成了全部工程.已知甲队单独完成此项工程所需的天数是乙队单独完成所需的天数的三分之二,则甲、乙两队单独完成各需多少天?
(2)甲工程队工作5天和乙工程队工作1天的费用和为34000元;甲工程队工作3天和乙工程队工作2天的费用和为26000元,则两队每天工作的费用各多少元?
(3)该公司现承接一项①中2倍的工程由两队去做,且甲、乙两队不在同一天内合做,又必须各自做整数天,试问甲、乙两队各需做多少天?若按②中的付费,你认为哪种方式付费最少?
(1)两队共同完成一项工程,乙队先单独做1天后,再由两队合做2天完成了全部工程.已知甲队单独完成此项工程所需的天数是乙队单独完成所需的天数的三分之二,则甲、乙两队单独完成各需多少天?
(2)甲工程队工作5天和乙工程队工作1天的费用和为34000元;甲工程队工作3天和乙工程队工作2天的费用和为26000元,则两队每天工作的费用各多少元?
(3)该公司现承接一项①中2倍的工程由两队去做,且甲、乙两队不在同一天内合做,又必须各自做整数天,试问甲、乙两队各需做多少天?若按②中的付费,你认为哪种方式付费最少?
考点:分式方程的应用,二元一次方程的应用,二元一次方程组的应用
专题:
分析:(1)题中由两个等量关系,“甲队单独完成工程所需的天数是乙队单独完成工程所需天数的
”,这是说明甲乙两队工作天数的关系,因此若设乙单独x天完成,则甲单独完成此工程的天数为
x;另一个等量关系:乙队先单独做1天后,再由两队合作2天就完成全部工程.可得:乙完成的工作量+甲乙合作完成的工作量=1;
(2)设甲工程队每天的费用是x元,甲工程队每天的费用是y元.等量关系:甲工程队工作5天和乙工程队工作1天的费用和为34000元;甲工程队工作3天和乙工程队工作2天的费用和为26000元;
(3)甲工程队工作x天,乙工程队工作y天,完成此项任务.则由题意得到:
x+
y=2,根据x、y都是整数进行解题.
| 2 |
| 3 |
| 2 |
| 3 |
(2)设甲工程队每天的费用是x元,甲工程队每天的费用是y元.等量关系:甲工程队工作5天和乙工程队工作1天的费用和为34000元;甲工程队工作3天和乙工程队工作2天的费用和为26000元;
(3)甲工程队工作x天,乙工程队工作y天,完成此项任务.则由题意得到:
| 1 |
| 4 |
| 1 |
| 6 |
解答:解:(1)设乙队单独完成此项工程需x天,则甲队完成此项工程需
x天,
根据题意得:
+2(
+
)=1,
解得 x=6,
则
x=4.
答:甲队完成此项工程需4天,乙队单独完成此项工程需6天;
(2)设甲工程队每天的费用是x元,甲工程队每天的费用是y元.
根据题意得:
,
解得
.
答:甲工程队每天的费用是6000元,乙工程队每天的费用是4000元;
(3)设甲工程队工作x天,乙工程队工作y天,完成此项任务.
根据题意得:
x+
y=2,
解得
或
或
,
答:甲工程队工作2天,乙工程队工作9天;
或者甲工程队工作4天,乙工程队工作6天;
甲工程队工作6天,乙工程队工作3天;
显然甲越小越好,故甲工程队工作2天,乙工程队工作9天付费最少,为2×6000+9×4000=48000元.
| 2 |
| 3 |
根据题意得:
| 1 |
| x |
| 1 |
| x |
| 3 |
| 2x |
解得 x=6,
则
| 2 |
| 3 |
答:甲队完成此项工程需4天,乙队单独完成此项工程需6天;
(2)设甲工程队每天的费用是x元,甲工程队每天的费用是y元.
根据题意得:
|
解得
|
答:甲工程队每天的费用是6000元,乙工程队每天的费用是4000元;
(3)设甲工程队工作x天,乙工程队工作y天,完成此项任务.
根据题意得:
| 1 |
| 4 |
| 1 |
| 6 |
解得
|
|
|
答:甲工程队工作2天,乙工程队工作9天;
或者甲工程队工作4天,乙工程队工作6天;
甲工程队工作6天,乙工程队工作3天;
显然甲越小越好,故甲工程队工作2天,乙工程队工作9天付费最少,为2×6000+9×4000=48000元.
点评:本题考查分式方程的应用、二元一次方程组的应用以及二元一次方程的应用.分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.此题涉及的公式:工作总量=工作效率×工作时间.

练习册系列答案
相关题目
 如图是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
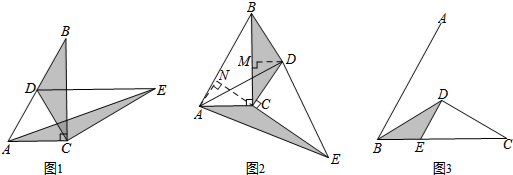
如图是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象. 已知:如图,BE=CF,AB=DE,AC=DF,求证:△ABC≌△DEF.
已知:如图,BE=CF,AB=DE,AC=DF,求证:△ABC≌△DEF. 已知点A(a,0)和B(0,b)满足(a-4)2+|b-6|=0,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
已知点A(a,0)和B(0,b)满足(a-4)2+|b-6|=0,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动. 如图,点P是正方形ABCD外一点,PD=6,△PAD的面积是36,△PCD的面积是15,则此正方形的边长是
如图,点P是正方形ABCD外一点,PD=6,△PAD的面积是36,△PCD的面积是15,则此正方形的边长是