题目内容
3.若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1<x2,有下列结论:①x1=2,x2=3;②m>-$\frac{1}{4}$;③x1<2<3<x2,
其中一定成立的结论有②.
分析 ①这只有在m=0时才能成立,故选项①错误;
②将已知的一元二次方程整理为一般形式,根据方程有两个不相等的实数根,得到根的判别式大于0,列出关于m的不等式,求出不等式的解集即可对选项②进行判断;
③当m=0时,x1=2,x2=3,故③错误.
解答 解:当m=0时,x1=2,x2=3,故③错误;
当m≠0时,x1≠2,x2≠3,故①错误;
∵方程有两个不相等的实数根x1、x2,
∴b2-4ac=(-5)2-4(6-m)=4m+1>0,
解得:m>-$\frac{1}{4}$,故选项②正确.
故答案为:②.
点评 此题考查了抛物线与x轴的交点,一元二次方程的解,以及根的判别式的运用,根据m的取值进行讨论是解题的关键.

练习册系列答案
相关题目
12.一个不透明的布袋里装有7个只有颜色不同的球,其中4个红球,3个白球,从布袋中随机摸出一个球,摸出的球是红球的概率是( )
| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
 点E是正方形ABCD的对角线BD上一点.∠AEF=90°,F在BC上,连接EC.求证:EF=EC.
点E是正方形ABCD的对角线BD上一点.∠AEF=90°,F在BC上,连接EC.求证:EF=EC.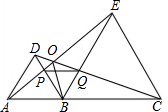 如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).
如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).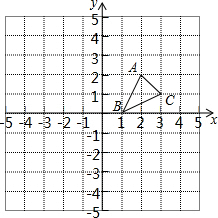 如图,平面直角坐标系中每个小方格均是边长为1个单位的正方形,△ABC的顶点均在格点上,点B的坐标为(1,0),按下列要求作图.
如图,平面直角坐标系中每个小方格均是边长为1个单位的正方形,△ABC的顶点均在格点上,点B的坐标为(1,0),按下列要求作图. 如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC.
如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC.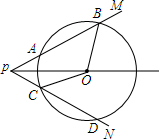 如图,点O是∠MPN的平分线上一点,以点O为圆心的圆和PM,PN分别相交于A,B,C,D四点,连接OB,OC.
如图,点O是∠MPN的平分线上一点,以点O为圆心的圆和PM,PN分别相交于A,B,C,D四点,连接OB,OC.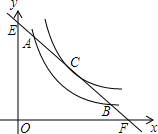 如图,直线y=-x+m与y=$\frac{4}{x}$只有唯一公共点C,与y=$\frac{k}{x}$交于A、B,且AC=$\frac{3}{2}$$\sqrt{2}$,求k.
如图,直线y=-x+m与y=$\frac{4}{x}$只有唯一公共点C,与y=$\frac{k}{x}$交于A、B,且AC=$\frac{3}{2}$$\sqrt{2}$,求k. 如图,在锐角△ABC中,以AB为直径的半圆分别交AC,BC于点E,F.
如图,在锐角△ABC中,以AB为直径的半圆分别交AC,BC于点E,F.