题目内容
13.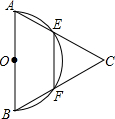 如图,在锐角△ABC中,以AB为直径的半圆分别交AC,BC于点E,F.
如图,在锐角△ABC中,以AB为直径的半圆分别交AC,BC于点E,F.(1)求证:EF=AB•cosC;
(2)若S△CEF=$\frac{1}{4}$S△ABC,求∠C的度数.
分析 (1)连接AF,根据圆内接四边形的性质得到∠CEF=∠B,∠C=○C,推出△CEF∽△CBA,根据相似三角形的性质得到$\frac{CF}{AC}=\frac{EF}{AB}$,根据圆周角定理得到∠AFB=90°,求得∠AFC=90°,即可得到结论;
(2)根据相似三角形的性质得$\frac{CF}{AC}$=$\frac{1}{2}$,于是得到cosC=$\frac{CF}{AC}$=$\frac{1}{2}$,即可得到结论.
解答  (1)证明:连接AF,
(1)证明:连接AF,
∵∠CEF=∠B,∠C=○C,
∴△CEF∽△CBA,
∴$\frac{CF}{AC}=\frac{EF}{AB}$,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠AFC=90°,
∴cosC=$\frac{CF}{AC}$,
即cosC=$\frac{EF}{AB}$,
∴EF=AB•cosC;
(2)解:∵△CEF∽△CBA,S△CEF=$\frac{1}{4}$S△ABC,
∴$\frac{CF}{AC}$=$\frac{1}{2}$,
∴cosC=$\frac{CF}{AC}$=$\frac{1}{2}$,
∴∠C=60°.
点评 本题主要考查对相似三角形的性质,圆周角定理,邻补角的定义,锐角三角函数的定义等知识点的理解和掌握,能熟练地运用相似三角形的性质和圆周角定理进行证明是解此题的关键.

练习册系列答案
相关题目
3.若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1<x2,有下列结论:
①x1=2,x2=3;②m>-$\frac{1}{4}$;③x1<2<3<x2,
其中一定成立的结论有②.
①x1=2,x2=3;②m>-$\frac{1}{4}$;③x1<2<3<x2,
其中一定成立的结论有②.
4.2015年9月30日杭州西湖景区某公园人流量为7万,每张门票80元,“十一黄金周”景区迎来了旅游高峰期,游客从各个省市来到杭州,该公园统计:十一黄金周期间,游客人数与前一天相比,增加和减少的情况如下表:(记增加为正).
(1)10月2号该公园的人流量是多少万人?
(2)“十一黄金周”期间,人流量最多和最少分别出现在哪一天?
(3)该公园的所有门票收入均要缴纳百分之五的税,求“十一黄金周”期间,该公园的实际收入.
| 日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 |
| 人数(万人) | +5 | -1.2 | +5.7 | -0.6 | +1.8 | -2.9 | -2.5 |
(2)“十一黄金周”期间,人流量最多和最少分别出现在哪一天?
(3)该公园的所有门票收入均要缴纳百分之五的税,求“十一黄金周”期间,该公园的实际收入.
18.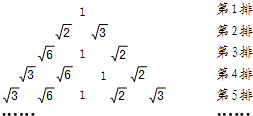 如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )
如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )
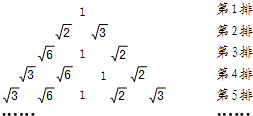 如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )
如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 3$\sqrt{2}$ |
5.下列各式中,属于分式的是( )
| A. | -$\frac{3}{5}$ | B. | $\frac{x{y}^{2}}{4}$ | C. | 6m2n3 | D. | $\frac{{b}^{2}}{a}$ |
 如图,△ABC与△A1B1C1关于直线l对称.若∠B1=35°,∠A=40°,则∠C的度数为105°.
如图,△ABC与△A1B1C1关于直线l对称.若∠B1=35°,∠A=40°,则∠C的度数为105°.