题目内容
14.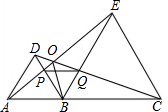 如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).
如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).
分析 易证△ABE≌△DBC,则有∠BAE=∠BDC,从而可证到△ABP≌△DBQ,则有AP=DQ,BP=BQ,由∠PBQ=60°可得△BPQ是等边三角形,则有PQ=PB.∠BPQ=60°,从而可得∠EPB>∠EBP,即可得到EB>EP,即EC>EP,由△ABE≌△DBC可得S△ABE=S△DBC,AE=DC,从而可得点B到AE、DC的距离相等,因而点B在∠AOC的角平分线上,即可得到∠AOB=∠BOC=∠COE=60°.
解答 解:∵△ABD和△BCE都是等边三角形,
∴BD=BA=AD,BE=BC=EC,∠ABD=∠CBE=60°,
∵点A、B、C在同一直线上,
∴∠DBE=180°-60°-60°=60°,
∴∠ABE=∠DBC=120°.
在△ABE和△DBC中,
$\left\{\begin{array}{l}{BD=BA}\\{∠ABE=∠DBC}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△DBC,
∴∠BAE=∠BDC.
在△ABP和△DBQ中,
$\left\{\begin{array}{l}{∠BAP=∠BDQ}\\{AB=DB}\\{∠ABP=∠DBQ=60°}\end{array}\right.$,
∴△ABP≌△DBQ,
∴AP=DQ,BP=BQ.
∴①正确.
∵∠PBQ=60°,
∴△BPQ是等边三角形,
∴PQ=PB.∠BPQ=60°.
∴③正确.
∵∠EPB>∠BPQ,∠BPQ=∠EBP=60°,
∴∠EPB>∠EBP,
∴EB>EP,
∴EC>EP,
∴②不正确.
∵∠DPA=∠PDO+∠DOP,∠DPA=∠PAB+∠ABP,∠PDO=∠PAB,
∴∠DOP=∠ABP=60°,
∴∠COE=60°,∠AOC=120°.
∵△ABE≌△DBC,
∴S△ABE=S△DBC,AE=DC,
∴点B到AE、DC的距离相等,
∴点B在∠AOC的角平分线上,
∴∠AOB=∠BOC=$\frac{1}{2}$∠AOC=60°,
∴∠AOB=∠BOC=∠COE=60°.
∴④正确.
故答案为①③④.
点评 本题主要考查了等边三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质、角平分线的判定、大角对大边等知识,根据到角两边距离相等的点在这个角的角平分线上,得到OB是∠AOC的角平分线,是证明④的关键.

①x1=2,x2=3;②m>-$\frac{1}{4}$;③x1<2<3<x2,
其中一定成立的结论有②.
| 日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 |
| 人数(万人) | +5 | -1.2 | +5.7 | -0.6 | +1.8 | -2.9 | -2.5 |
(2)“十一黄金周”期间,人流量最多和最少分别出现在哪一天?
(3)该公园的所有门票收入均要缴纳百分之五的税,求“十一黄金周”期间,该公园的实际收入.
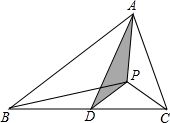 如图,△ABC中,D是BC边的中点,已知点P是△ACD内一点,己知△ACP的面积为7,△ABP的面积为13,则阴影部分的面积为3.
如图,△ABC中,D是BC边的中点,已知点P是△ACD内一点,己知△ACP的面积为7,△ABP的面积为13,则阴影部分的面积为3.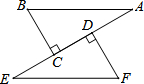 如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证:
如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证: