题目内容
13.定义:如果一元二次方程ax2+bx+c=0(a≠0),满足a+b+c=O,那么我们称这样的方程为“风凰”方程.已知:ax2+bx+c=0(a≠0)是“风凰”方程.
求证:1必是该方程的一个根(用两种不同方法证明)
分析 方法一:由“风凰”方程的定义,可知ax2+bx+c=0满足a+b+c=0,可得:当x=1时,有a+b+c=0.故问题可证明;
方法二:将c=-a-b代入原方程左边,再将方程左边因式分解即可.
解答 证明:方法一:∵ax2+bx+c=0(a≠0)是“风凰”方程,
∴a+b+c=0,即a×12+b×1+c=0,
∴1必是该方程的一个根;
方法二:∵ax2+bx+c=0(a≠0)是“风凰”方程,
∴a+b+c=0,
∴c=-a-b,
原方程化为ax2+bx-a-b=0,
即a(x+1)(x-1)+b(x-1)=0,
∴(x-1)(ax+a+b)=0,
∴1必是该方程的一个根.
点评 本题考查了一元二次方程的解的定义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了因式分解法解一元二次方程.

练习册系列答案
相关题目
3.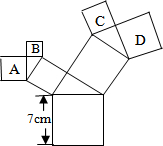 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.
 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.| A. | 3cm2 | B. | 4cm2 | C. | 7cm2 | D. | 49cm2 |
8.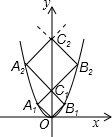 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )| A. | 2013 | B. | 2014 | C. | 2013$\sqrt{2}$ | D. | 2014$\sqrt{2}$ |
5.下列各数化简后为正数的是( )
| A. | +(-2) | B. | -(-2) | C. | -(+2) | D. | -|-2| |
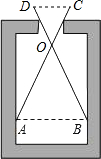 如图,用一个交叉卡钳(OA=OB,OC=OD)测量零件的内孔直径AB,若OC:OA=1:2,且量的CD=12mm,则零件的内孔直径AB是24mm.
如图,用一个交叉卡钳(OA=OB,OC=OD)测量零件的内孔直径AB,若OC:OA=1:2,且量的CD=12mm,则零件的内孔直径AB是24mm. 如图,?ABCD中,对角线AC、BD相交于点O,点E是CD的中点,则△DOE与△BCD的面积比为1:4.
如图,?ABCD中,对角线AC、BD相交于点O,点E是CD的中点,则△DOE与△BCD的面积比为1:4.