题目内容
8.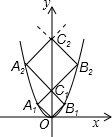 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )| A. | 2013 | B. | 2014 | C. | 2013$\sqrt{2}$ | D. | 2014$\sqrt{2}$ |
分析 根据正方形对角线平分一组对角可得OB1与y轴的夹角为45°,然后表示出OB1的解析式,再与抛物线解析式联立求出点B1的坐标,然后求出OB1的长,再根据正方形的性质求出OC1,表示出C1B2的解析式,与抛物线联立求出B2的坐标,然后求出C1B2的长,再求出C1C2的长,然后表示出C2B3的解析式,与抛物线联立求出B3的坐标,然后求出C2B3的长,从而根据边长的变化规律解答即可.
解答 解:∵OA1C1B1是正方形,
∴OB1与y轴的夹角为45°,
∴OB1的解析式为y=x,
联立方程组得:$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
∴B点的坐标是:(1,1);
OB1=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
同理可得:正方形C1A2C2B2的边长C1B2=2$\sqrt{2}$;
…
依此类推,正方形则正方形C2013A2014C2014B2014的边长为2014$\sqrt{2}$.
故选:D.
点评 考查了二次函数的对称性,正方形的性质,表示出正方形的边长所在直线的解析式,与抛物线解析式联立求出正方形的顶点的坐标,从而求出边长是解题的关键.

练习册系列答案
相关题目
19.反比例函数y=$\frac{3}{x}$的图象不一定经过点( )
| A. | (-3,1) | B. | (-3,-1) | C. | (1,3) | D. | ($\frac{3}{2}$,2) |
16.已知扇形的圆心角为60°,半径为5,则扇形的周长为( )
| A. | $\frac{5}{3}$π | B. | $\frac{5}{3}$π+10 | C. | $\frac{5}{6}$ | D. | $\frac{5}{6}$π+10 |
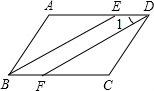 如图,四边形ABCD是平行四边形,∠ABC=78°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F,求∠1的度数为39°.
如图,四边形ABCD是平行四边形,∠ABC=78°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F,求∠1的度数为39°.