题目内容
3．
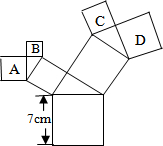如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积之和为（ ）cm2．| A． | 3cm2 | B． | 4cm2 | C． | 7cm2 | D． | 49cm2 |
分析 根据正方形的面积公式，连续运用勾股定理，发现：四个小正方形的面积和等于最大正方形的面积．
解答 
解：∵所有的三角形都是直角三角形，所有的四边形都是正方形，
∴正方形A的面积=a2，正方形B的面积=b2，
正方形C的面积=c2，正方形D的面积=d2，
又∵a2+b2=x2，c2+d2=y2，
∴正方形A、B、C、D的面积和=（a2+b2）+（c2+d2）=x2+y2=72=49cm2．
故选：D．
点评 本题考查了勾股定理．有一定难度，注意掌握直角三角形中，两直角边的平方和等于斜边的平方．
练习册系列答案
相关题目
15．若（x-2）（x+3）=x2+ax+b，则a、b的值分别为（ ）
| A． | a=5，b=6 | B． | a=1，b=-6 | C． | a=1，b=6 | D． | a=5，b=-6 |
如图，在△ABC中，BC边上有n个点（包括B、C两点），则图中共有多少个三角形？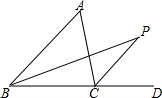
已知在△ABC中，内角∠ABC的平分线与外角∠ACD的平分线交于点P，试说明：∠P=$\frac{1}{2}$∠A．
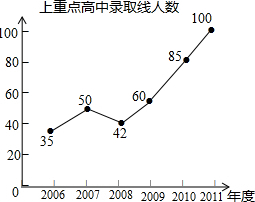某校近6年来中考上市重点高中录取的情况如图所示：
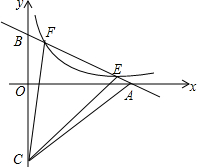如图，直线y=-$\frac{1}{2}$x+b（b＞0）与双曲线y=$\frac{1}{x}$（x＞0）交于E、F两点，与x轴、y轴分别交于A、B两点，点C（0，-$\frac{3}{2}$b），连接CA，CB，CE，CF，若S△CEF=2（S△CAE+S△CBF），求b的值．
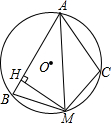如图，⊙O的内接四边形ABMC中，AB＞AC，M是$\widehat{BC}$的中点，MH⊥AB于N，求证：BH=$\frac{1}{2}$（AB-AC）．