题目内容
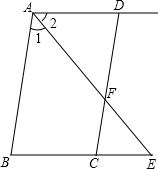 如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:∵AB∥DC(已知)
∴∠1=∠CFE(
∵AE平分∠BAD(已知)
∴∠1=∠2 (角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=
∴AD∥BC (
考点:平行线的判定与性质
专题:推理填空题
分析:由AB与DC平行,利用两直线平行同位角相等得到一对角相等,再由AE为角平分线,得到一对角相等,再根据已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答:证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠E;内错角相等,两直线平行.
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠E;内错角相等,两直线平行.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
相关题目
对于反比例函数y=
(k<0),下列说法正确的是( )
| k |
| x |
| A、图象经过点(1,-k) |
| B、图象位于第一、三象限 |
| C、图象是中心对称图形 |
| D、当x<0时,y随x的增大而减小 |
下列方程无实数根的是( )
| A、x2=0 |
| B、x2-1=0 |
| C、x2+1=0 |
| D、x2-x=0 |
 已知直线y=
已知直线y=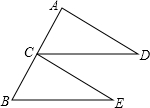 如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE.
如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE.