Question

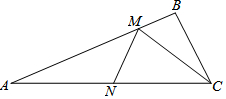
11．如图，△ABC中，∠ACB=45°，边AB上一定点P，M、N分别是AC和BC边上的动点，当△PMN的周长最短时，∠MPN的度数是90°．

Answer 1

分析 根据对称的性质，易求得∠C+∠EPF=180°，由∠ACB=45°，易求得∠D+∠G=45°，继而求得答案．

解答 解：∵PD⊥AC，PG⊥BC，
∴∠PEC=∠PFC=90°，
∴∠C+∠EPF=180°，
∵∠C=45°，
∴∠EPF=135°，
∵∠D+∠G+∠EPF=180°，
∴∠D+∠G=45°，
由对称可知：∠G=∠GPN，∠D=∠DPM，
∴∠GPN+∠DPM=45°，
∴∠MPN=135°-45°=90°，
故答案为：90°

点评 此题考查了最短路径问题以及线段垂直平分线的性质．关键是注意掌握数形结合思想的应用．