题目内容
6.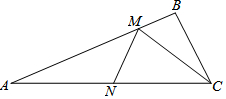 如图:△ABC中,AC=$\sqrt{6}$,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=$\sqrt{6}$,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 3 |
分析 作C关于AB的对称点E,过E作EN⊥AC于N,连接AE,则EN=CM+MN的最小值,由对称的性质得到AB垂直平分BC,推出△AEN是等腰直角三角形,解直角三角形即可得到结论.
解答 解:作C关于AB的对称点E,过E作EN⊥AC于N,连接AE,
则EN=CM+MN的最小值,
由对称的性质得:AB垂直平分EC,
∴AE=AC=$\sqrt{6}$,∠EAC=2∠BAC=45°,
∴△AEN是等腰直角三角形,
∴EN=$\frac{\sqrt{2}}{2}$AE=$\sqrt{3}$,
故选B
点评 本题考查的是轴对称-最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过线段平分线性质,垂线段最短,确定线段和的最小值.

练习册系列答案
相关题目
1.下列各组数中,互为相反数的是( )
| A. | |-$\frac{1}{3}$|和-$\frac{1}{3}$ | B. | |-$\frac{1}{3}$|和-3 | C. | |-$\frac{1}{3}$|和$\frac{1}{3}$ | D. | |-$\frac{1}{3}$|和3 |
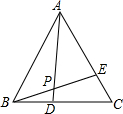 如图,已知等边△ABC中,DC=EA,AD与BE相交于点P,求∠APB的度数.
如图,已知等边△ABC中,DC=EA,AD与BE相交于点P,求∠APB的度数. 如图,△ABC中,∠ACB=45°,边AB上一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最短时,∠MPN的度数是90°.
如图,△ABC中,∠ACB=45°,边AB上一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最短时,∠MPN的度数是90°. 已知:线段AB=8cm,点C是AB的中点,点D是AC的中点,求线段BD的长.
已知:线段AB=8cm,点C是AB的中点,点D是AC的中点,求线段BD的长. 如图,一艘客轮沿东北方向OC行驶,在海上O处发现灯塔A在北偏西30°方向上,灯塔B在南偏东60°方向上.
如图,一艘客轮沿东北方向OC行驶,在海上O处发现灯塔A在北偏西30°方向上,灯塔B在南偏东60°方向上. 如图,在七巧板中找出一组互相平行的线段GL∥BC和一组互相垂直的线段EK⊥AC.
如图,在七巧板中找出一组互相平行的线段GL∥BC和一组互相垂直的线段EK⊥AC.