题目内容
2. 如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2cm,OA=60cm,OB=15cm,则火焰AC的长度为8cm.
如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2cm,OA=60cm,OB=15cm,则火焰AC的长度为8cm.
分析 连接AC、BD,可证明△AOC∽△BOD,根据相似三角形的性质可得$\frac{AC}{DB}$=$\frac{AO}{BO}$,代入相应数据进行计算即可.
解答 解:连接AC、BD,
∵CA⊥AB,DB⊥AB,
∴∠CAO=∠DBO=90°,
∵∠COA=∠DOB,
∴△AOC∽△BOD,
∴$\frac{AC}{DB}$=$\frac{AO}{BO}$,
∵BD=2cm,OA=60cm,OB=15cm,
∴$\frac{AC}{2}$=$\frac{60}{15}$,
解得:AC=8cm,
答:火焰AC的长度为8cm.
故答案为:8cm.
点评 此题主要考查了相似三角形的应用,关键是掌握相似三角形,对应边成比例.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
12.一个圆锥的母线长为 4,侧面展开图是半圆,则圆锥的侧面积是( )
| A. | 2π | B. | 4π | C. | 8π | D. | 16π |
10.若A(a1,b1),B(a2,b2)是反比例函数y=$\frac{1}{x}$(x>0)图象上的两个点,且a1<a2,则b1与b2的大小关系是( )
| A. | b1>b2 | B. | b1=b2 | C. | b1<b2 | D. | 大小不确定 |
7. 电信部门要再S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在( )
电信部门要再S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在( )
 电信部门要再S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在( )
电信部门要再S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在( )| A. | ∠COD的平分线上任意某点处 | |
| B. | 线段AB的垂直平分线上任意某点处 | |
| C. | ∠COD的平分线和线段AB的交点处 | |
| D. | ∠COD的平分线和线段AB垂直平分线的交点处 |
12.实验中学积极开展大课间活动,组织了一次踢毽子比赛,每班派5名学生参加.按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,如表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个),经统计发现两班总分相等,此时有学生建议,可通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)根据上表提供的数据填写如表:
(2)根据以上信息,你认为应该把冠军发给哪一个班级?简述理由.
(3)现在若想派一支代表队外出参加一次比赛,根据以往经验,个人超过115个才有可能获奖,则应该选派哪个代表队?简述理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 86 | 100 | 98 | 119 | 97 | 500 |
| 优秀率 | 中位数 | 方差 | |
| 甲班 | 60% | 100 | 46.8 |
| 乙班 | 40% | 98 | 114 |
(3)现在若想派一支代表队外出参加一次比赛,根据以往经验,个人超过115个才有可能获奖,则应该选派哪个代表队?简述理由.
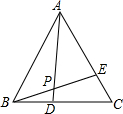 如图,已知等边△ABC中,DC=EA,AD与BE相交于点P,求∠APB的度数.
如图,已知等边△ABC中,DC=EA,AD与BE相交于点P,求∠APB的度数. 如图,△ABC中,∠ACB=45°,边AB上一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最短时,∠MPN的度数是90°.
如图,△ABC中,∠ACB=45°,边AB上一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最短时,∠MPN的度数是90°.