题目内容
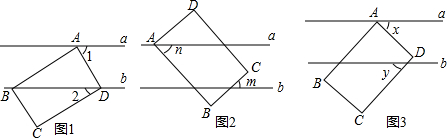
7.如图1,Rt△ABC中,∠B=90°,AB=BC=2,点O是边AC上一动点,⊙O切AB于点D.(1)当⊙O与BC相切时,求⊙O的半径;
(2)当点C落在⊙O上时,求⊙O的半径;
(3)如图2,在AB边上取点E,使得BE=AD,以EB为边向下作矩形EGHB,EB:BH=1:$\sqrt{3}$,作直线EH
①当O,E,H三点共线时,求⊙O的半径;
②直线EH与⊙O相切时,求⊙O的半径.

分析 (1)如图1中,当⊙O与BC相切时,设点E为切点,连接OD、OE,只要证明四边形ODBE是正方形即可解决问题.
(2)如图2中,当⊙O经过点C时,设半径为r,由OA+OC=AC列出方程即可解决问题.
(3)①如图3中,连接OD,设半径为r,由AD+DE+EB=2,列出方程即可解决.
②如图4中,当EH与⊙O相切于点M,连接OD,OM,OE.设半径为r,由AD+DE+EB=2,列出方程即可解决.如图5中,设⊙O的半径为r,EH与⊙O相切于点M,连接OM,OD,OE,由AE+ED+EB=2,列出方程即可解决.
解答 解:(1)如图1中,当⊙O与BC相切时,设点E为切点,连接OD、OE.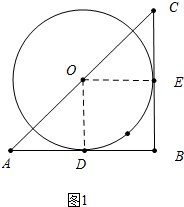
∵∠ODB=∠OEB=∠B=90°,
∴四边形ODBE是矩形,
∵OD=OE,
∴四边形ODBE是正方形,
∴DB=OE=OD,
∵BA=BC=2,
∴∠A=∠AOD=45°,
∴AD=OD,
∴AD=DB=1,
∴OD=1,
(2)如图2中,当⊙O经过点C时,设半径为r,由OA+OC=AC,可得$\sqrt{2}$r+r=2$\sqrt{2}$,
∴r=4-2$\sqrt{2}$.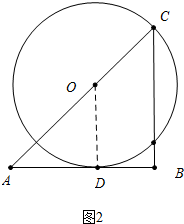
(3)①如图3中,连接OD.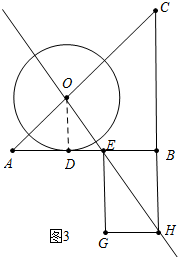
∵EB:BH=1:$\sqrt{3}$,
∴∠BEH=∠ODE=60°,设半径为r,
∵AD+DE+EB=2,
∴r+$\frac{\sqrt{3}}{3}$r+r=2,
∴r=$\frac{12-2\sqrt{3}}{11}$.
②如图4中,当EH与⊙O相切于点M,连接OD,OM,OE.设半径为r.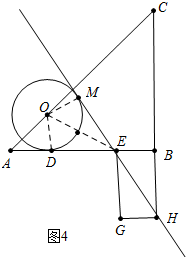
∵OD=OM,OD⊥EA,OM⊥ME,
∴∠OED=∠OEM=30°,
∵AD+DE+EB=2,
∴r+$\sqrt{3}$r+r=2,
∴r=4-2$\sqrt{3}$.
如图5中,设⊙O的半径为r,EH与⊙O相切于点M,连接OM,OD,OE.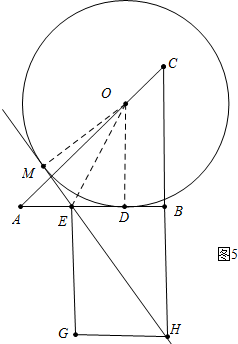
∵OM=OD,OM⊥EM,OD⊥DE,
∴∠OEM=∠OED=60°,
∵AE+ED+EB=2,
∴2r-$\frac{\sqrt{3}}{3}$r=2,
∴r=$\frac{12+2\sqrt{3}}{11}$.
点评 本题考查圆的综合题、等腰直角三角形的性质、矩形的性质、特殊角的三角函数等知识,解题的关键是学会利用参数,把问题转化为方程解决,属于中考压轴题.

| A. | x>1 | B. | x<1 | C. | x≤1 | D. | x≥1 |
 阅读材料:
阅读材料: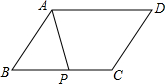 如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,
如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$, 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.