Question

12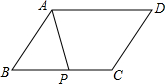．如图，在平行四边形ABCD中，点P是BC边的中点，设$\overrightarrow{CD}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b$，
（1）试用向量$\overrightarrow a，\overrightarrow b$表示向量$\overrightarrow{AP}$，那么$\overrightarrow{AP}$=$-\overrightarrow a+\frac{1}{2}\overrightarrow b$；
（2）在图中求作：$\overrightarrow{AB}-\overrightarrow{BP}$． （保留作图痕迹，不要求写作法，写出结果）．

Answer 1

分析 （1）求出$\widehat{AB}$，$\widehat{BP}$，根据$\widehat{AB}$=$\widehat{AB}$+$\widehat{BP}$，即可求出$\overrightarrow{AP}$，
（2）如图$\overrightarrow{AB}-\overrightarrow{BP}$=$\overrightarrow{AB}$-$\overrightarrow{AE}$=$\overrightarrow{EB}$．

解答 解：（1）在平行四边形ABCD中，$\overrightarrow{BA}=\overrightarrow{CD}=\overrightarrow{a}$，$\overrightarrow{BC}=\overrightarrow{AD}=\overrightarrow{b}$，
∵点P是BC的中点，
∴$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}$，
∴$\overrightarrow{AB}=-\overrightarrow{BA}$，$\overrightarrow{AB}+\overrightarrow{BP}=\overrightarrow{AP}$
∴$\overrightarrow{AP}=-\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$，
（2）如图：$\overrightarrow{AB}-\overrightarrow{BP}$=$\overrightarrow{AB}$-$\overrightarrow{AE}$=$\overrightarrow{EB}$，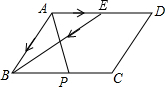

$\overrightarrow{EB}$就是所求的向量．
故答案为：$-\overrightarrow a+\frac{1}{2}\overrightarrow b$．

点评 本题是基础题，考查向量的加减法的运算，注意向量的和与差后仍然是一个向量．