题目内容
17.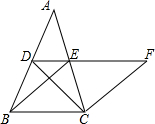 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.(1)求证:四边形BCFE是菱形;
(2)在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).
分析 (1)由题意易得,EF与BC平行且相等,故四边形BCFE是平行四边形.又邻边EF=BE,则四边形BCFE是菱形;
(2)根据平行线的性质、三角形的面积公式解答即可.
解答 (1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC,BC=2DE.
∵CF∥BE,
∴四边形BCFE是平行四边形.
∵BE=2DE,BC=2DE,
∴BE=BC.
∴?BCFE是菱形;
(2)解:①∵由(1)知,四变形BCFE是菱形,
∴BC=FE,BC∥EF,
∴△FEC与△BEC是等底等高的两个三角形,
∴S△FEC=S△BEC.
②△AEB与△BEC是等底同高的两个三角形,则S△AEB=S△BEC.
③S△ADC=$\frac{1}{2}$S△ABC,S△BEC=$\frac{1}{2}$S△ABC,则它S△ADC=S△BEC.
④S△BDC=$\frac{1}{2}$S△ABC,S△BEC=$\frac{1}{2}$S△ABC,则它S△BDC=S△BEC.
综上所述,与△BEC面积相等的三角形有:△FEC、△AEB、△ADC、△BDC.
点评 此题主要考查菱形的性质和判定以及三角形面积的计算,使学生能够灵活运用菱形知识解决有关问题.

练习册系列答案
相关题目
5.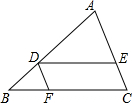 如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )
如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )
 如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )
如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )| A. | $\frac{AD}{DB}$=$\frac{DE}{BF}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ | C. | $\frac{AE}{CE}$=$\frac{BF}{CF}$ | D. | $\frac{CE}{AC}$=$\frac{BF}{BC}$ |
 作图题(只保留作图痕迹,不写作法)
作图题(只保留作图痕迹,不写作法)
 如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和