题目内容
9.(1)计算:3($\sqrt{3}$-π)0-$\frac{\sqrt{20}-\sqrt{15}}{\sqrt{5}}$+(-1)2011(2)先化简,再求值:$\frac{3}{x-3}$-$\frac{18}{x^2-9}$,其中x=$\sqrt{10}$-3.
分析 (1)根据0指数幂的计算法则、数的乘方法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=3-$\frac{2\sqrt{5}-\sqrt{15}}{\sqrt{5}}$-1
=3-2+$\sqrt{3}$-1
=$\sqrt{3}$;
(2)原式=$\frac{3(x+3)-18}{(x-3)(x+3)}$
=$\frac{3x-9}{(x-3)(x+3)}$
=$\frac{3(x-3)}{(x-3)(x+3)}$
=$\frac{3}{x+3}$,
当x=$\sqrt{10}$-3时,原式=$\frac{3}{\sqrt{10}-3+3}$=$\frac{3\sqrt{10}}{10}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
19.2015年9月20日,吉图珺高铁正式开通运营,使长春至军春通勤时间缩短至3小时左右,项目总投资416亿元,416亿这个数用科学记数法表示为( )
| A. | 416×108 | B. | 41.6×109 | C. | 4.16×1010 | D. | 4.16×1011 |
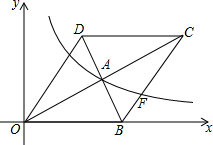 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点A的坐标是(8,4).
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点A的坐标是(8,4).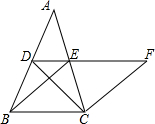 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.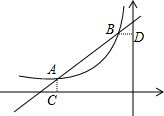 如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.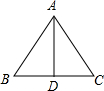 如图,等边△ABC中,AD为高,若AB=6,则CD的长度为3.
如图,等边△ABC中,AD为高,若AB=6,则CD的长度为3.