题目内容
12.如果平行四边形的一边长是14,那么它的两条对角线的长可以是( )| A. | 16和12 | B. | 16和18 | C. | 18或10 | D. | 36或6 |
分析 由平行四边形的性质和三角形的三边关系容易得出A、C、D不正确,B正确,即可得出结论.
解答 解:如图所示:
∵四边形ABCD是平行四边形,
∴OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD;
∵在△OAB中,OA=8,OB=6,
OA+OB=8+6=14=AB,
∴A不正确;
∵OA=8,OB=9,OA+OB>OA,
∴B正确;
∵OA=9,OB=5,OA+OB=AB,
∴C不正确;
∵OA=18,OB=3,AB+OB<OA,
∴D不正确.
故选:B.
点评 本题考查了平行四边形的想、三角形的三边关系定理;熟练掌握平行四边形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
3. 如图,将△ABC绕顶点A逆时针旋转30°得到△ADE.若此时BC的对应边DE恰好经过点C,且AE⊥AB,则∠B的度数为( )
如图,将△ABC绕顶点A逆时针旋转30°得到△ADE.若此时BC的对应边DE恰好经过点C,且AE⊥AB,则∠B的度数为( )
 如图,将△ABC绕顶点A逆时针旋转30°得到△ADE.若此时BC的对应边DE恰好经过点C,且AE⊥AB,则∠B的度数为( )
如图,将△ABC绕顶点A逆时针旋转30°得到△ADE.若此时BC的对应边DE恰好经过点C,且AE⊥AB,则∠B的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
20.解关于x的方程$\frac{x-6}{x-1}$=$\frac{m}{x-1}$产生增根,则常数m的值等于( )
| A. | -7 | B. | -5 | C. | -3 | D. | 1 |
7.下列选项中是一元二次方程的为( )
| A. | x+2=0 | B. | x-2y=1 | C. | x2-2x-3=0 | D. | $\frac{1}{x}$+3=1 |
4.若|x-1|+|y+2|+|z-3|=0,则(x-1)(y+2)(z+3)的值是( )
| A. | 48 | B. | -48 | C. | 0 | D. | 无法计算 |
1.下列总有意义的分式是( )
| A. | $\frac{{{x^2}-{y^2}}}{x-y}$ | B. | $\frac{x+y}{{{x^2}+{y^2}}}$ | C. | $\frac{2x}{{{x^2}+1}}$ | D. | $\frac{{{x^2}+x}}{x+1}$ |
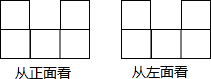 桌上摆着一个由若干个相同正方体组成的几何体,其从正面看和从左面看得到的形状如图所示,那么这个几何体最多可以由13个正方体组成,最少可以由5个正方体组成.
桌上摆着一个由若干个相同正方体组成的几何体,其从正面看和从左面看得到的形状如图所示,那么这个几何体最多可以由13个正方体组成,最少可以由5个正方体组成.