题目内容
2.新苑小区的物业管理部门为了美化环境,在小区靠墙的一侧设计了一处长方形花圃(墙长25m),三边外围用篱笆围起,栽上蝴蝶花,共用篱笆40m,(1)花圃的面积能达到180m2吗?
(2)花圃的面积能达到250m2吗?
如果能,请你给出设计方案;如果不能,请说明理由.
分析 设BC=xm,则AB=$\frac{1}{2}$(40-x)m,花圃的面积为$\frac{1}{2}$x(40-x).(1)(2)假设花圃的面积能达到180 m2,250m2,只需令$\frac{1}{2}$x(40-x)等于200或250,判断所列方程是否有解,若有解求出x的值,即花圃的面积能达到,否则不能达到;
解答 解:(1)设BC=xm,则AB=$\frac{1}{2}$(40-x)=(20-$\frac{1}{2}$x)m
①由题意得:
x(20-$\frac{1}{2}$x)=180,
x2-40x+360=0,
△=402-4×360=0,
解之得,x=20m
答:能达到200m2.
(2)x(20-$\frac{1}{2}$x)=250,
x2-40x+500=0,
△=402-4×500=-400<0,
即:此方程无解,
答:不能达到250m2
点评 本题主要考查一元二次方程的应用,关键在于理解清楚题意,找出等量关系列出方程求解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13.下列整式乘法的运算中,正确的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+b2 | C. | (a+b)(a-b)=2a | D. | (a-b)2=a2-2ab-b |
14.下列函数,其图象经过点(2,2)的是( )
| A. | y=3x | B. | y=1-2x | C. | y=$\frac{4}{x}$ | D. | y=x2-1 |
11.计算:
(1)$\sqrt{18}$-($\sqrt{3}$+1)0+(-1)2
(2)$\frac{1}{{2+\sqrt{3}}}+\sqrt{27}-6\sqrt{\frac{1}{3}}$.
(1)$\sqrt{18}$-($\sqrt{3}$+1)0+(-1)2
(2)$\frac{1}{{2+\sqrt{3}}}+\sqrt{27}-6\sqrt{\frac{1}{3}}$.
12.如果平行四边形的一边长是14,那么它的两条对角线的长可以是( )
| A. | 16和12 | B. | 16和18 | C. | 18或10 | D. | 36或6 |
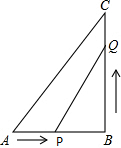 已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.