题目内容
10.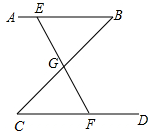 如图,公园里有一条“Z”形的林荫小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一条石凳E、G、F,且G恰好为BC的中点,E、G、F三点在同一条直线上,点G与F之间有一座假山,而使得两处不能直接到达.你能想出测量G、F之间距离的方法吗?说明其中的道理.
如图,公园里有一条“Z”形的林荫小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一条石凳E、G、F,且G恰好为BC的中点,E、G、F三点在同一条直线上,点G与F之间有一座假山,而使得两处不能直接到达.你能想出测量G、F之间距离的方法吗?说明其中的道理.
分析 根据两直线平行,内错角相等可得∠B=∠C,然后利用“角边角”证明△CFG和△BEG全等,根据全等三角形对应边相等可得EG=FG,从而得解.
解答 解:测量出E、G之间的距离即为G、F之间的距离.
理由如下:∵AB∥CD,
∴∠B=∠C,
∵G恰好为BC的中点,
∴BG=CG,
在△CFG和△BEG中,$\left\{\begin{array}{l}{∠B=∠C}\\{BG=CG}\\{∠BGE=∠CGF}\end{array}\right.$,
∴△CFG≌△BEG(ASA),
∴EG=FG,
故,E、G之间的距离即为G、F之间的距离.
点评 本题考查了全等三角形的应用,平行线的性质,熟练掌握三角形全等的判定方法并准确识图确定出全等三角形是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
5.下列运算正确的是( )
| A. | 3a+2a=6a | B. | a2+a3=a5 | C. | a6÷a2=a4 | D. | a2•a4=a8 |
6.下列命题是假命题的是( )
| A. | 三角形的内心到三角形三条边的距离相等 | |
| B. | 三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等 | |
| C. | 对于实数a,b,若|a|≤|b|,则a≤b | |
| D. | 对于实数x,若$\sqrt{{x}^{2}}$=x,则x≥0 |
3.四边形ABCD中,∠A=∠C,∠B=∠D,如果再添加一个条件,即可推出该四边形是菱形,那么这个条件可以是( )
| A. | ∠D=90° | B. | AC=BD | C. | AB=AC | D. | 以上都不行 |
5.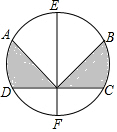 如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )
如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )
 如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )
如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )| A. | 9π | B. | 3π | C. | 6π | D. | $\frac{9}{4}$π |
2.已知二次函数y=ax2+bx+c自变量x与函数值y之间满足下列数量关系,那么(a+b+c)($\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$)的值是24.
| x | 3 | 5 | 7 |
| y | 0.08 | 0.08 | 3 |
19.某超市在春节期间对顾客实行优惠,规定如下:
(1)刘老师一次性购物600元,求他实际付款多少元?
(2)若顾客在该超市一次性购物x元(x≥500),实际付款y元,请求出用含x的代数式表示y的式子.
(3)如果刘老师两次购物贷款合计820元,第一次购物的贷款为a元(200<a<300),用含a的代数式表示:两次购物刘老师实际多少元?
| 一次性购物 | 优惠方法 |
| 少于200元 | 不予优惠 |
| 低于500元但不低于200元 | 九折优惠 |
| 500元或超过500元 | 其中500元部分给予九折优惠,超过500元部分给予八折优惠 |
(2)若顾客在该超市一次性购物x元(x≥500),实际付款y元,请求出用含x的代数式表示y的式子.
(3)如果刘老师两次购物贷款合计820元,第一次购物的贷款为a元(200<a<300),用含a的代数式表示:两次购物刘老师实际多少元?
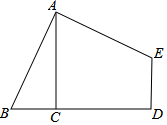 如图,AC⊥BD于C,∠D=90°,AB=AE且AB⊥AE,四边形ABDE的面积为36,则AC=6.
如图,AC⊥BD于C,∠D=90°,AB=AE且AB⊥AE,四边形ABDE的面积为36,则AC=6.