题目内容
15.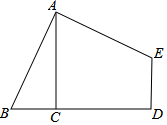 如图,AC⊥BD于C,∠D=90°,AB=AE且AB⊥AE,四边形ABDE的面积为36,则AC=6.
如图,AC⊥BD于C,∠D=90°,AB=AE且AB⊥AE,四边形ABDE的面积为36,则AC=6.
分析 如图作EF⊥AC于F,连接EC.由△ABC≌△EAF,推出AC=EF,设AC=EF=x,由四边形EFCD是矩形,推出S△EFC=S△ECD,由S△ABC=S△EAF,推出S△ACE=$\frac{1}{2}$•S四边形ABDE=18,列出方程即可解决问题.
解答 解:如图作EF⊥AC于F,连接EC.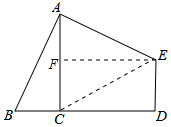
∵BA⊥AE,AC⊥BD,
∴∠BAE=∠BCA=90°,
∴∠BAC+∠B=90°,∠EAF+∠BAC=90°,
∴∠B=∠EAF,
在△ABC和△EAF中,
$\left\{\begin{array}{l}{∠ACB=∠AFE}\\{∠B=∠EAF}\\{AB=AE}\end{array}\right.$,
∴△ABC≌△EAF,
∴AC=EF,设AC=EF=x,
∵∠EFC=∠FCD=∠D=90°,
∴四边形EFCD是矩形,
∴S△EFC=S△ECD,∵S△ABC=S△EAF,
∴S△ACE=$\frac{1}{2}$•S四边形ABDE=18,
∴$\frac{1}{2}$•x•x=18,
∴x=6或-6(舍弃),
∴AC=6.
故答案为6.
点评 本题考查全等三角形的判定和性质,矩形的判定和性质、三角形的面积公式等知识,解题的关键是正确寻找全等三角形解决问题,学会用转化的思想思考问题,把四边形问题转化为三角形问题,属于中考常考题型.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
10.不等式2x+3>3x+2的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
11.下列命题是真命题的是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线相等的四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
20.无论a取何值,下列代数式的值总是正数的有( )
|a+1|,a2+3,a+100,|a|+1,a2n+1(n是整数)
|a+1|,a2+3,a+100,|a|+1,a2n+1(n是整数)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 对于自变量x的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.分段函数在不同的定义域上,函数的表达式也不同.例如:y=$\left\{\begin{array}{l}{{x}^{2}-2x(x≥0)}\\{2x(x<0)}\end{array}\right.$是分段函数.当x≥0时,它是二次函数y=x2-2x,当x<0时,它是正比例函数y=2x.
对于自变量x的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.分段函数在不同的定义域上,函数的表达式也不同.例如:y=$\left\{\begin{array}{l}{{x}^{2}-2x(x≥0)}\\{2x(x<0)}\end{array}\right.$是分段函数.当x≥0时,它是二次函数y=x2-2x,当x<0时,它是正比例函数y=2x.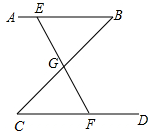 如图,公园里有一条“Z”形的林荫小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一条石凳E、G、F,且G恰好为BC的中点,E、G、F三点在同一条直线上,点G与F之间有一座假山,而使得两处不能直接到达.你能想出测量G、F之间距离的方法吗?说明其中的道理.
如图,公园里有一条“Z”形的林荫小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一条石凳E、G、F,且G恰好为BC的中点,E、G、F三点在同一条直线上,点G与F之间有一座假山,而使得两处不能直接到达.你能想出测量G、F之间距离的方法吗?说明其中的道理. 如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD=$\frac{4}{3}$.
如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD=$\frac{4}{3}$.