Question

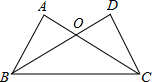如图，已知∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB的角平分线，BD、AC相交于点O，求证：△ABC≌△DCB．

Answer 1

考点：全等三角形的判定

专题：证明题

分析：首先根据角平分线的性质可得∠ACB=

1

2

∠DCB，∠DBC=

1

2

∠ABC，进而得到∠ACB=∠DBC，然后再根据ASA证明△ABC≌△DCB．

解答：证明：∵BD、CA分别是∠ABC、∠DCB的角平分线，
∴∠ACB=

1

2

∠DCB，∠DBC=

1

2

∠ABC，
∵∠ABC=∠DCB，
∴∠ACB=∠DBC，
在△ABC和△DCB中

∠ABC=∠DCB CB=CB ∠ACB=∠DBC

，
∴△ABC≌△DCB（ASA）．

点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．