题目内容
一元二次方程x2+3=2x的根的情况为（ ）
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、有一个实数根 |
| D、没有实数根 |
考点：根的判别式
专题：
分析：先把方程化为一般式，再计算判别式，然后根据判别式的意义判断方程根的情况即可．
解答：解：∵方程化为一般式得x2-2x+3=0，
∴△=（-2）2-4×1×3=-8＜0，
∴方程没有实数根．
故选D．
∴△=（-2）2-4×1×3=-8＜0，
∴方程没有实数根．
故选D．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
阅读快车系列答案
相关题目
?ABCD中，对角线AC和BC相交于O，若AC=10，BD=14，则AB的取值范围是（ ）
| A、2＜AB＜12 |
| B、10＜AB＜12 |
| C、5＜AB＜7 |
| D、4＜AB＜24 |
方程x（x+3）=x+3的解为（ ）
| A、x1=0，x2=-3 |
| B、x1=1，x2=-3 |
| C、x1=0，x2=3 |
| D、x1=1，x2=3 |
小红在月历的同一列上圈出相邻的三个数，若算出它们的和是39，则该列第一个数是（ ）
| A、6 | B、12 | C、13 | D、14 |
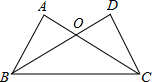如图，已知∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB的角平分线，BD、AC相交于点O，求证：△ABC≌△DCB．