题目内容
14．
如图，点A，C，D，B在同一直线上，CF平分∠GCB，CF∥DE，若∠ACG为α度，则∠EDB为（90-$\frac{α}{2}$）度（用含α的式子表示）
分析 根据CF∥DE得出∠EDB=∠BCF，再由互补和角平分线的定义得出∠BCF=$\frac{1}{2}$（180°-α），解答即可．
解答 解：∵点A，C，D，B在同一直线上，∠ACG为α度，
∴∠GCB=180°-α，
∵CF平分∠GCB，
∴∠FCB=$\frac{1}{2}$（180°-α），
∵CF∥DE，
∴∠EDB=∠BCF=90-$\frac{α}{2}$．
故答案为：（90-$\frac{α}{2}$）．
点评 此题考查平行线的性质，关键是根据平行线得出∠EDB=∠BCF和利用角平分线的定义解答．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
5．
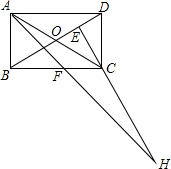在矩形ABCD中，AB=1，AD=$\sqrt{3}$，AF平分∠DAB，过C点作CE⊥BD于E，延长AF、EC交于点H，下列结论中正确的是（ ）
①AF=$\frac{1}{2}$FH；②BO=BF；③CA=CH；④BE=3ED．
在矩形ABCD中，AB=1，AD=$\sqrt{3}$，AF平分∠DAB，过C点作CE⊥BD于E，延长AF、EC交于点H，下列结论中正确的是（ ）①AF=$\frac{1}{2}$FH；②BO=BF；③CA=CH；④BE=3ED．
| A． | ②③ | B． | ③④ | C． | ①②④ | D． | ②③④ |
9．
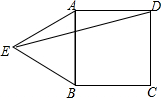如图，点E是正方形ABCD外一点，EA=4，EB=3，且∠AEB=45°，则ED的长为（ ）
如图，点E是正方形ABCD外一点，EA=4，EB=3，且∠AEB=45°，则ED的长为（ ）| A． | $\sqrt{23}$ | B． | 2$\sqrt{10}$ | C． | $\sqrt{41}$ | D． | 5$\sqrt{2}$ |
19．已知a＜b，下列不等式中，变形正确的是（ ）
| A． | a-3＞b-3 | B． | $\frac{a}{3}$＞$\frac{b}{3}$ | C． | 3a-1＞3b-1 | D． | -3a＞-3b |