题目内容
2.方程组$\left\{\begin{array}{l}x-z=4\\ x-2y=1\\ 3y+z=2\end{array}\right.$经“消元”后可得到一个关于x、y的二元一次方程组为$\left\{\begin{array}{l}{x-2y=1}\\{x+3y=6}\end{array}\right.$..分析 先把第1个方程和第3个方程相加消去z,然后把所得的新方程和第2个方程组成方程组即可.
解答 解:$\left\{\begin{array}{l}{x-z=4①}\\{x-2y=1②}\\{3y+z=2③}\end{array}\right.$,
①+③得x+3y=6④,
由②④组成方程组得$\left\{\begin{array}{l}{x-2y=1}\\{x+3y=6}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{x-2y=1}\\{x+3y=6}\end{array}\right.$.
点评 本题考查了解三元一次方程组:利用加减消元法或代入消元法把解三元一次方程组的问题转化为解二元一次方程组的问题.

练习册系列答案
相关题目
14. 如图,要使AD∥BC,那么可以选择下列条件中的( )
如图,要使AD∥BC,那么可以选择下列条件中的( )
 如图,要使AD∥BC,那么可以选择下列条件中的( )
如图,要使AD∥BC,那么可以选择下列条件中的( )| A. | ∠1+∠B=180° | B. | ∠2=∠3 | C. | ∠1=∠4 | D. | ∠B=∠D |
14. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高BH=( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高BH=( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高BH=( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高BH=( )| A. | 4.6 | B. | 4.8 | C. | 5 | D. | 5.2 |
10.估计$\sqrt{56}$的值在哪两个整数之间( )
| A. | 55和57 | B. | 6和7 | C. | 7和8 | D. | 8和9 |
 如图,点A,C,D,B在同一直线上,CF平分∠GCB,CF∥DE,若∠ACG为α度,则∠EDB为(90-$\frac{α}{2}$)度(用含α的式子表示)
如图,点A,C,D,B在同一直线上,CF平分∠GCB,CF∥DE,若∠ACG为α度,则∠EDB为(90-$\frac{α}{2}$)度(用含α的式子表示) 如图,在?ABCD中,∠B=70°,则∠D=70°.
如图,在?ABCD中,∠B=70°,则∠D=70°.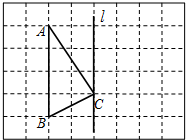 如图,在正方形网格中,△ABC的三个顶点都在方格图的格点上.请画出△A'B'C',使△A'B'C'和△ABC关于直线l成轴对称.
如图,在正方形网格中,△ABC的三个顶点都在方格图的格点上.请画出△A'B'C',使△A'B'C'和△ABC关于直线l成轴对称.