题目内容
5.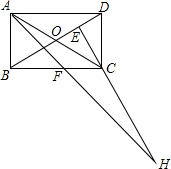 在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )
在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )①AF=$\frac{1}{2}$FH;②BO=BF;③CA=CH;④BE=3ED.
| A. | ②③ | B. | ③④ | C. | ①②④ | D. | ②③④ |
分析 求出OA=OC=OD=BD,求出∠ADB=30°,求出∠ABO=60°,得出等边三角形AOB,求出AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,根据以上结论推出即可.
解答 解: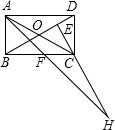 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AD=$\sqrt{3}$,AB=1,
∴tan∠ADB=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠ADB=30°,
∴∠ABO=60°,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,
∴△ABO是等边三角形,
∴AB=BO,∠AOB=∠BAO=60°=∠COE,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=BO,
∴BF=BO,
∴②正确;
∵∠BAO=60°,∠BAF=45°,
∴∠CAH=15°,
∵CE⊥BD,
∴∠CEO=90°,
∵∠EOC=60°,
∴∠ECO=30°,
∴∠H=∠ECO-∠CAH=30°-15°=15°=∠CAH,
∴AC=CH,
∴③正确;
作HG⊥BC的延长线于点G,
∵AB=1,AD=$\sqrt{3}$,
∴BC=CH=2,
∴HG=CH•cos∠CHG=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∵△ABF∽△HGF,
∴$\frac{AB}{HG}=\frac{AF}{FH}$,
即$\frac{1}{\sqrt{3}}$=$\frac{AF}{FH}$,
∴FH=$\sqrt{3}$FA,
∴AF=$\frac{1}{2}$FH错误,
故①错误;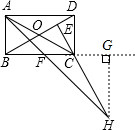
∵△AOB是等边三角形,
∴AO=OB=AB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,
∵CE⊥BD,
∴DE=EO=$\frac{1}{2}$DO=$\frac{1}{2}$BD,
即BE=3ED,∴④正确;
即正确的有②③④3个,
故选D.
点评 本题考查了矩形的性质,平行线的性质,角平分线定义,定义三角形的性质和判定,等边三角形的性质和判定等知识点的综合运用,难度偏大,对学生提出较高的要求.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 7.3×10-4m | B. | 7.3×10-5m | C. | 7.3×10-6m | D. | 7.3×-5m |
| A. | 4和5 | B. | 5和6 | C. | 6和7 | D. | 7和8 |
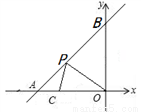
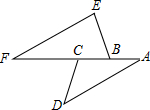 如图,已知点A、B、C、F在同一条直线上,AD∥EF,∠D=40°,∠F=30°,那么∠ACD的度数是110°.
如图,已知点A、B、C、F在同一条直线上,AD∥EF,∠D=40°,∠F=30°,那么∠ACD的度数是110°.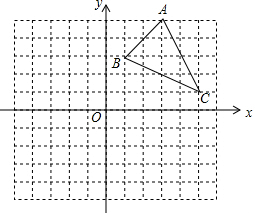 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1). 如图,点A,C,D,B在同一直线上,CF平分∠GCB,CF∥DE,若∠ACG为α度,则∠EDB为(90-$\frac{α}{2}$)度(用含α的式子表示)
如图,点A,C,D,B在同一直线上,CF平分∠GCB,CF∥DE,若∠ACG为α度,则∠EDB为(90-$\frac{α}{2}$)度(用含α的式子表示)