题目内容
13.我们把由不平行于底的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”.如图1,四边形ABCD即为“准等腰梯形”,其中∠B=∠C,(1)在图1所示的“准等腰梯形”ABCD中,选择合适的一个顶点引一条直线将四边形ABCD分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形(画出一种示意图即可);
(2)在由不平行于BC的直线AD截△PBC所得的四边形ABCD中,∠BAD与∠ADC的平分线交于点E.若EB=EC,请问当点E在四边形ABCD内部时(即图2所示情形),四边形ABCD是不是“准等腰梯形”,为什么?若点E不在四边形ABCD内部时,情况又将如何?写出你的结论.(不必说明理由)

分析 (1)根据条件∠B=∠C和梯形的定义就可以画出图形;
(2)根据角平分线的性质可以得出△EFB≌△EHC,就可以得出∠3=∠4,再由条件就可以得出∠ABC=∠DCB,从而得出结论,当点E不在四边形内部时分两种情况讨论就可以求出结论.
解答 解:(1)如图1,过点D作DE∥BC交PB于点E,则四边形ABCD分割成一个等腰梯形BCDE和一个三角形ADE;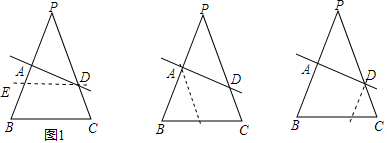
(2)作EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,如图2: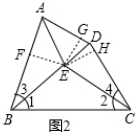
∴∠BFE=∠CHE=90°.
∵AE平分∠BAD,DE平分∠ADC,
∴EF=EG=EH,
在Rt△EFB和Rt△EHC中,
$\left\{\begin{array}{l}{BE=CE}\\{EF=EH}\end{array}\right.$,
∴Rt△EFB≌Rt△EHC(HL),
∴∠3=∠4.
∵BE=CE,
∴∠1=∠2.
∴∠1+∠3=∠2+∠4
即∠ABC=∠DCB,
∵ABCD为AD截某三角形所得,且AD不平行BC,
∴ABCD是“准等腰梯形”.
当点E不在四边形ABCD的内部时,有两种情况:
如图3,当点E在BC边上时,同理可以证明△EFB≌△EHC,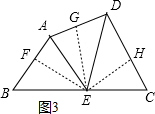
∴∠B=∠C,
∴ABCD是“准等腰梯形”.
当点E在四边形ABCD的外部时,
四边形ABCD不一定是“准等腰梯形”.
分两种情况:
情况一:
当∠BED的角平分线与线段BC的垂直平分线重合时,四边形ABCD为“准等腰梯形”;
情况二:
当∠BED的角平分线与线段BC的垂直平分线相交时,四边形ABCD不是“准等腰梯形”.
点评 本题考查了平行线的性质的运用,相似三角形的判定及性质的运用,角平分线的性质的运用,全等三角形的判定及性质的运用,解答时多次运用角平分线的性质是关键.

练习册系列答案
相关题目
4.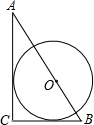 如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
 如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )| A. | $\frac{24}{7}$ | B. | 4 | C. | 5 | D. | 2 |
1. 如图,在△ABC中,点O为重心,则S△DOE:S△BOC=( )
如图,在△ABC中,点O为重心,则S△DOE:S△BOC=( )
 如图,在△ABC中,点O为重心,则S△DOE:S△BOC=( )
如图,在△ABC中,点O为重心,则S△DOE:S△BOC=( )| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 2:3 |
 如图,AC∥BD,AD、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.
如图,AC∥BD,AD、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.