题目内容
2. 如图,AC∥BD,AD、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.
如图,AC∥BD,AD、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.
分析 由平行线分线段成比例定理得出$\frac{EF}{AC}=\frac{BF}{AB}$,$\frac{EF}{BD}=\frac{AF}{AB}$,证出$\frac{EF}{AC}+\frac{EF}{BD}=\frac{BF}{AB}+\frac{AF}{AB}$=1,即可得出结论.
解答 证明:∵AC∥BD,EF∥BD,
∴$\frac{EF}{AC}=\frac{BF}{AB}$,$\frac{EF}{BD}=\frac{AF}{AB}$,
∴$\frac{EF}{AC}+\frac{EF}{BD}=\frac{BF}{AB}+\frac{AF}{AB}$=$\frac{BF+AF}{AB}$=1,
∴$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.
点评 此题考查了平行线分线段成比例定理;熟练掌握平行线分线段成比例定理,找准对应关系是本题的关键.

练习册系列答案
相关题目
12.下列各式中,y是x的二次函数的是( )
| A. | y=2x+1 | B. | y=-2x+1 | C. | y=x2+2 | D. | y=$\frac{1}{2}$x-2 |
10.某校以年级为单位开展广播操比赛,全年级有10个班,每个班有50名学生,规定每班抽25名学生参加比赛,这时样本容量是( )
| A. | 10 | B. | 50 | C. | 500 | D. | 250 |
7.在Rt△ABC中,∠C=90°,若cosA=$\frac{5}{13}$,则sinB的值是( )
| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |

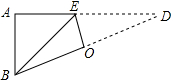 如图,直角△ABD中,∠A=90°,AB=3cm,AD=9cm,将此三角形折叠,使点B与点D重合,折痕为EO,则△EOD的面积为$\frac{15}{4}$cm2.
如图,直角△ABD中,∠A=90°,AB=3cm,AD=9cm,将此三角形折叠,使点B与点D重合,折痕为EO,则△EOD的面积为$\frac{15}{4}$cm2.