如图.在△ABC中.点O为重心.则S△DOE:S△BOC=( )A．1:4B．1:3C．1:2D．2:3 题目和参考答案——青夏教育精英家教网—

题目内容

1．

如图，在△ABC中，点O为重心，则S_△DOE：S_△BOC=（　　）

A．

1：4

B．

1：3

C．

1：2

D．

2：3

分析利用三角形重心的定义得出D是AB的中点，E是AC的中点，进而得出△DOE∽△COB，再利用相似三角形的性质得出答案．

解答解：∵点O为重心，
∴D是AB的中点，E是AC的中点，
∴DE∥BC，$\frac{DO}{CO}$=$\frac{1}{2}$，
∴△DOE∽△COB，
∴S_△DOE：S_△BOC=1：4．
故选：A．

点评此题主要考查了相似三角形的判定与性质以及重心的定义，得出△DOE∽△COB是解题关键．

练习册系列答案

小学生10分钟口算测试100分系列答案

相关题目

11．已知点P（m+2，2m-5）在y轴上，则P点的坐标是（0，-9）．

12．下列各式中，y是x的二次函数的是（　　）

9．下列运算中正确的有（　　）个．
①$\sqrt{（-4）^{2}}$=±4 ②$\root{3}{-\frac{27}{64}}$=-$\frac{3}{4}$ ③$\sqrt{3}+\sqrt{2}=\sqrt{5}$ ④$\sqrt{1{0}^{-6}}$=0.001．

16．

如图，已知AB=AD，BC=DC，AC与BD交于点E．请写出三个不同类型的正确结论．（不添加字母和辅助线，不要求证明）

6．某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：

排数	1	2	3	4
座位数	50	53	56	59

按这种方式排下去，
（1）第5、6排各有多少个座位？
（2）第n排有多少个座位？
（3）根据（2）的代数式，判断第25排有多少个座位？

13．我们把由不平行于底的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”．如图1，四边形ABCD即为“准等腰梯形”，其中∠B=∠C，
（1）在图1所示的“准等腰梯形”ABCD中，选择合适的一个顶点引一条直线将四边形ABCD分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形（画出一种示意图即可）；
（2）在由不平行于BC的直线AD截△PBC所得的四边形ABCD中，∠BAD与∠ADC的平分线交于点E．若EB=EC，请问当点E在四边形ABCD内部时（即图2所示情形），四边形ABCD是不是“准等腰梯形”，为什么？若点E不在四边形ABCD内部时，情况又将如何？写出你的结论．（不必说明理由）

10．某校以年级为单位开展广播操比赛，全年级有10个班，每个班有50名学生，规定每班抽25名学生参加比赛，这时样本容量是（　　）

11．

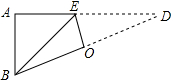如图，直角△ABD中，∠A=90°，AB=3cm，AD=9cm，将此三角形折叠，使点B与点D重合，折痕为EO，则△EOD的面积为$\frac{15}{4}$cm²．

试题分类