题目内容
15.如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,动点P从点B出发,沿射线BC的方向以每秒ycm的速度运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).(1)当y=2时,t为何值时,四边形PQDC是平行四边形?
(2)当四边形PQDC为菱形时,求y,t的值;
(3)当t=2时,是否存在点P,使△PQD为等腰三角形?若存在,请求出所有满足要求的y的值;若不存在,请说明理由.

分析 (1)由题意已知,AD∥BC,要使四边形PQDC是平行四边形,则只需要让QD=PC即可,因为Q、P点的速度已知,AD、BC的长度已知,要求时间,用时间=路程÷速度,即可求出时间;
(3)使△PQD是等腰三角形,可分三种情况,即PQ=PD、PQ=QD、QD=PD;可利用等腰三角形及直角梯形的性质,分别用y表达等腰三角形的两腰长,再利用两腰相等即可求得y
解答 解:(1)当y=2时,
∵四边形PQDC是平行四边形
∴DQ=CP
当P从B运动到C时,
∵DQ=AD-AQ=16-t,
CP=21-2t
∴16-t=21-2t
解得t=5
当P从C运动到B时,
∵DQ=AD-AQ=16-t,
CP=2t-21
∴16-t=2t-21,
解得t=$\frac{37}{3}$,
∴当t=5或$\frac{37}{3}$秒时,四边形PQDC是平行四边形
(2)如图1,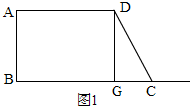
过点D作DG⊥BC,
在Rt△DGC中,CG=21-15=5,DG=AB=12,
根据勾股定理得,CD=13
由运动得,AQ=t,BP=ty,
∴QD=16-t,PC=21-ty,
∵四边形PQDC为菱形,而DQ∥PC
∴QD=PC=CD,
∴16-t=21-ty=13,
∴t=3,y=$\frac{8}{3}$;
(3)当t=2时,
∴AQ=2,BP=2y,
∴QD=AD-AQ=16-2=14,PC=21-2y
当PQ=PD时,
如图2,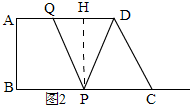
作PH⊥AD于H,则HQ=HD
∵QH=HD=$\frac{1}{2}$QD=7,
∵AH=BP,
∴AQ+QH=BP,
∴2+7=2y,
∴y=$\frac{9}{2}$
当PQ=QD时QH=AH-AQ=BP-AQ=2y-2,QD=14,
∵PQ2=QH2+PH2=(2y-2)2+122,
∴196=(2y-2)2+122,
∴y=1+$\sqrt{13}$或y=1-$\sqrt{13}$(舍)
解得y=1+$\sqrt{13}$;
当QD=PD时DH=AD-AH=AD-BP=16-2y,
∵QD2=PD2=PH2+HD2=122+(16-2y)
∴196=122+(16-2y)2
∴y=8-$\sqrt{13}$或y=8+$\sqrt{13}$(舍)
综上可知,当y=$\frac{9}{2}$或y=1+$\sqrt{13}$或y=8-$\sqrt{13}$时,△PQD是等腰三角形.
点评 此题是四边形综合题,主要考查了直角梯形的性质、平行四边形的性质、菱形的判定、等腰三角形的性质,特别应该注意要全面考虑各种情况,不要遗漏.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案| 用电量(度) | 100 | 140 | 150 | 180 | 200 |
| 户数 | 3 | 4 | 6 | 5 | 2 |
| A. | 153 | B. | 154 | C. | 160 | D. | 180 |
| A. | 1:3 | B. | 3:1 | C. | 1:$\sqrt{3}$ | D. | $\sqrt{3}$:1 |
 如图,菱形ABCD的对角线AC,BD交于点O,过点O作EF⊥AD,分别交AD,BC于点E,F,若AC=6,BD=8,则EF长为( )
如图,菱形ABCD的对角线AC,BD交于点O,过点O作EF⊥AD,分别交AD,BC于点E,F,若AC=6,BD=8,则EF长为( )
 如图,点C在线段BD上,AB⊥BD,PD⊥BD,∠B=∠D=90°,AB=3,BC=6,CD=2,则当DE=1或4时,△ABC与△CDE相似.
如图,点C在线段BD上,AB⊥BD,PD⊥BD,∠B=∠D=90°,AB=3,BC=6,CD=2,则当DE=1或4时,△ABC与△CDE相似.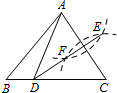 如图,在△ABC中,分别以点A、C为圆心,以大于$\frac{AC}{2}$长为半径作圆弧,两弧分别相交于点E、F,连结EF并延长交边BC于点D,连结AD.若AB=6,BC=8,则△ABD的周长为( )
如图,在△ABC中,分别以点A、C为圆心,以大于$\frac{AC}{2}$长为半径作圆弧,两弧分别相交于点E、F,连结EF并延长交边BC于点D,连结AD.若AB=6,BC=8,则△ABD的周长为( )