题目内容
 如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=| 12 |
| 13 |
考点:解直角三角形
专题:计算题
分析:在Rt△ADC中,利用正弦的定义得sinC=
=
,则可设AD=12x,所以AC=13x,利用勾股定理计算出DC=5x,由于cos∠DAC=sinC得到tanB=
,接着在Rt△ABD中利用正切的定义得到BD=13x,所以13x+5x=12,解得x=
,然后利用AD=12x进行计算.
| AD |
| AC |
| 12 |
| 13 |
| 12 |
| 13 |
| 2 |
| 3 |
解答:解:在Rt△ADC中,sinC=
=
,
设AD=12x,则AC=13x,
∴DC=
=5x,
∵cos∠DAC=sinC=
,
∴tanB=
,
在Rt△ABD中,∵tanB=
=
,
而AD=12x,
∴BD=13x,
∴13x+5x=12,解得x=
,
∴AD=12x=8.
故答案为8.
| AD |
| AC |
| 12 |
| 13 |
设AD=12x,则AC=13x,
∴DC=
| AC2-AD2 |
∵cos∠DAC=sinC=
| 12 |
| 13 |
∴tanB=
| 12 |
| 13 |
在Rt△ABD中,∵tanB=
| AD |
| BD |
| 12 |
| 13 |
而AD=12x,
∴BD=13x,
∴13x+5x=12,解得x=
| 2 |
| 3 |
∴AD=12x=8.
故答案为8.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
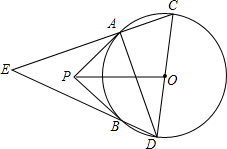 如图,PA,PB是⊙O的两条切线,切线分别是A,B.CD是⊙O的直径,直线AC,BD相交于点E.
如图,PA,PB是⊙O的两条切线,切线分别是A,B.CD是⊙O的直径,直线AC,BD相交于点E.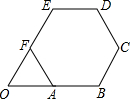 如图,正六边形ABCDEF的边长为2
如图,正六边形ABCDEF的边长为2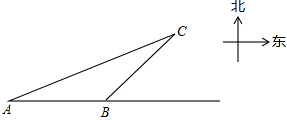 一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?
一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近? 已知,如图,MN是⊙O的弦,AB是⊙O的直径,AB⊥MN,垂足为点P,半径OC,OD分别交MN于点E,F,且OE=OF.求证:
已知,如图,MN是⊙O的弦,AB是⊙O的直径,AB⊥MN,垂足为点P,半径OC,OD分别交MN于点E,F,且OE=OF.求证:
 如图,直线AB,CD相交于点E,FE⊥AB,若∠FEC-∠AEC=20°,那么∠AED的度数是
如图,直线AB,CD相交于点E,FE⊥AB,若∠FEC-∠AEC=20°,那么∠AED的度数是 a、b两数在一条隐去原点的数轴上的位置如图所示,①a-b<0;②a+b<0;③ab<0;④(a+1)(b+1)<0,上述4个式子中一定成立的是
a、b两数在一条隐去原点的数轴上的位置如图所示,①a-b<0;②a+b<0;③ab<0;④(a+1)(b+1)<0,上述4个式子中一定成立的是