题目内容
 如图,直线AB,CD相交于点E,FE⊥AB,若∠FEC-∠AEC=20°,那么∠AED的度数是
如图,直线AB,CD相交于点E,FE⊥AB,若∠FEC-∠AEC=20°,那么∠AED的度数是考点:对顶角、邻补角,垂线
专题:
分析:设∠AEC为x,则∠FEC=x+20°;由∠AEC+∠FEC=90°,得出x+x+20°=90°,求出x=35°,即可求出∠AED=180°-35°=145°.
解答:解:设∠AEC为x,则∠FEC=x+20°;
∵EF⊥AB,
∴∠AEF=90°,
∴∠AEC+∠FEC=90°,
∴x+x+20°=90°,
解得:x=35°,
即∠AEC=35°,
∴∠AED=180°-35°=145°;
故答案为:145°.
∵EF⊥AB,
∴∠AEF=90°,
∴∠AEC+∠FEC=90°,
∴x+x+20°=90°,
解得:x=35°,
即∠AEC=35°,
∴∠AED=180°-35°=145°;
故答案为:145°.
点评:本题考查了对顶角、邻补角以及垂线的定义;仔细观察图形弄清角之间的互余、互补关系是解题的关键.

练习册系列答案
相关题目
下列各图象中,不能表示y是x的函数的是( )
A、 |
B、 |
C、 |
D、 |
 △ABC中,BF、CF是角平分线,∠A=70°,则∠BFC=( )
△ABC中,BF、CF是角平分线,∠A=70°,则∠BFC=( )| A、125° | B、110° |
| C、100° | D、150° |
 如图,在△ABC中,点E在BC边上,点F在AC边的延长线上,AF=BE,连接FE并延长,交AB边于点D,求证:
如图,在△ABC中,点E在BC边上,点F在AC边的延长线上,AF=BE,连接FE并延长,交AB边于点D,求证: 如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC= 如图,AO⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数.
如图,AO⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数. 已知如图,⊙O的内接△ABC中,AB=AC,弦BD,CE分别∠ABC,∠ACB,且BE=BC,求证:五边形AEBCD是正五边形.
已知如图,⊙O的内接△ABC中,AB=AC,弦BD,CE分别∠ABC,∠ACB,且BE=BC,求证:五边形AEBCD是正五边形. 如图,A,B是⊙O上的两点,∠AOB=120°,C是
如图,A,B是⊙O上的两点,∠AOB=120°,C是
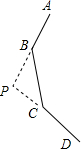 如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n.
如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n.