题目内容
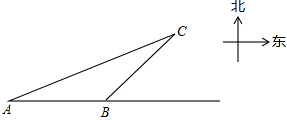 一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?
一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?考点:解直角三角形的应用-方向角问题
专题:
分析:过C作AB的垂线,交直线AB于点D,设CD=x海里,在Rt△ACD与Rt△BCD中用含x的代数式分别表示AD与BD,根据AD-BD=AB列出方程
x-x=60,解方程求出x的值,从而求得BD的值,问题得解.
| 3 |
解答: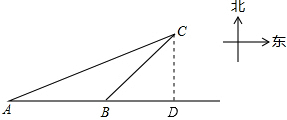 解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
设CD=x海里,
在Rt△BCD中,∵tan∠CBD=
,
∴BD=
=x.
在Rt△ACD中,∵tanA=
,
∴AD=
=
x.
∵AD-BD=AB,
∴
x-x=60,
解得x=30(
+1),
∴BD=30(
+1).
答:轮船继续向东航行30(
+1)海里,距离小岛C最近.
 解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.设CD=x海里,
在Rt△BCD中,∵tan∠CBD=
| CD |
| BD |
∴BD=
| x |
| tan45° |
在Rt△ACD中,∵tanA=
| CD |
| AD |
∴AD=
| x |
| tan30° |
| 3 |
∵AD-BD=AB,
∴
| 3 |
解得x=30(
| 3 |
∴BD=30(
| 3 |
答:轮船继续向东航行30(
| 3 |
点评:本题考查了解直角三角形的应用-方向角问题,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
用四舍五入法要求对0.07019分别取近似值,其中错误的是( )
| A、0.1(精确到0.1) |
| B、0.07(精确到百分位) |
| C、0.07(精确到千分位) |
| D、0.0702(精确到0.0001) |
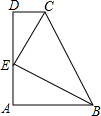 如图,CD∥AB,CE平分∠BCD,BE平分∠ABC,过点E作直线垂直CD于点D,交AB于点A,则下列关系式中成立的有( )
如图,CD∥AB,CE平分∠BCD,BE平分∠ABC,过点E作直线垂直CD于点D,交AB于点A,则下列关系式中成立的有( )①
| CD |
| AD |
| DE |
| AE |
| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |
| A、2个 | B、3个 | C、4个 | D、5个 |
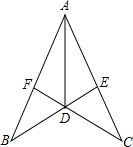 如图,若AB=AC,BE=CF,CF⊥AB,BE⊥AC,则图中全等的三角形共有( )对.
如图,若AB=AC,BE=CF,CF⊥AB,BE⊥AC,则图中全等的三角形共有( )对.| A、5对 | B、4对 | C、3对 | D、2对 |
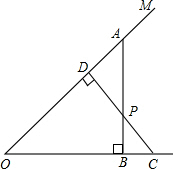 如图,AB⊥ON于点B,CD⊥OM于点D,AB与CD相交于点P,则下列说法错误的是( )
如图,AB⊥ON于点B,CD⊥OM于点D,AB与CD相交于点P,则下列说法错误的是( )| A、线段AB的长是点A到ON的距离 |
| B、线段CD的长是点C到OM的距离 |
| C、线段PD的长是点P到OM的距离 |
| D、线段PB是点P到ON的距离 |
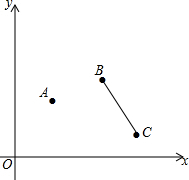 平面直角坐标系中,已知:A(2,3),B(4,4),C(5,1),在x轴上找一点D,使四边形ABCD的周长最小.
平面直角坐标系中,已知:A(2,3),B(4,4),C(5,1),在x轴上找一点D,使四边形ABCD的周长最小. 如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC= 已知如图,⊙O的内接△ABC中,AB=AC,弦BD,CE分别∠ABC,∠ACB,且BE=BC,求证:五边形AEBCD是正五边形.
已知如图,⊙O的内接△ABC中,AB=AC,弦BD,CE分别∠ABC,∠ACB,且BE=BC,求证:五边形AEBCD是正五边形. 如图,AB为⊙O的直径,CD为弦,AB=10,CD∥AB,CD=6.
如图,AB为⊙O的直径,CD为弦,AB=10,CD∥AB,CD=6.