题目内容
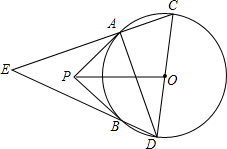 如图,PA,PB是⊙O的两条切线,切线分别是A,B.CD是⊙O的直径,直线AC,BD相交于点E.
如图,PA,PB是⊙O的两条切线,切线分别是A,B.CD是⊙O的直径,直线AC,BD相交于点E.(1)当直径CD绕圆心旋转时,∠E的大小与∠P有关系吗?如果有,找出这个数量关系并说明理由.
(2)如果∠E=30°,PA=6,求⊙O的半径.
考点:切线的性质
专题:
分析:(1)∠P=2∠E;连接OA、OB,先证明∠E=90°-∠BDA,再证明∠AOB=2∠BDA,∠P=180°-∠AOB,即可证出∠P=2∠E.
(2)连接AB,作OF⊥AB于的F,先证明△PAB是等边三角形,得出AB=PA=6,AF=
AB=3,再求出∠AOF=60°,根据锐角三角函数求出AO即可.
(2)连接AB,作OF⊥AB于的F,先证明△PAB是等边三角形,得出AB=PA=6,AF=
| 1 |
| 2 |
解答:解:(1)有关系,∠P=2∠E;
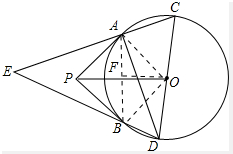
理由如下:连接OA、OB,如图所示:
 ∵CD为直径,
∵CD为直径,
∴∠CAD=90°,
∴∠E=90°-∠BDA,
∵∠BDA与∠BOA对的弧为
,
∴∠AOB=2∠BDA,
∵PA、PB分别切⊙O于点A、B,
∴∠PAO=∠PBO=90°,
∴∠P=180°-∠AOB,
∴∠P=180°-2∠BDA=2(90°-∠BDA),
∴∠P=2∠E.
(2)连接AB,作OF⊥AB于的F,如图所示:
∵∠E=30°,
∴∠P=60°,
∴∠AOB=120°,
∵PA=PB,
∴△PAB是等边三角形,
∴AB=PA=6,
∴AF=
AB=3,
∵∠AOF=
=60°,
∴AO=
=
=2
,
即⊙O的半径为2
.
理由如下:连接OA、OB,如图所示:
 ∵CD为直径,
∵CD为直径,∴∠CAD=90°,
∴∠E=90°-∠BDA,
∵∠BDA与∠BOA对的弧为
 |
| AB |
∴∠AOB=2∠BDA,
∵PA、PB分别切⊙O于点A、B,
∴∠PAO=∠PBO=90°,
∴∠P=180°-∠AOB,
∴∠P=180°-2∠BDA=2(90°-∠BDA),
∴∠P=2∠E.
(2)连接AB,作OF⊥AB于的F,如图所示:
∵∠E=30°,
∴∠P=60°,
∴∠AOB=120°,
∵PA=PB,
∴△PAB是等边三角形,
∴AB=PA=6,
∴AF=
| 1 |
| 2 |
∵∠AOF=
| 120° |
| 2 |
∴AO=
| AF |
| sin∠AOF |
| 3 | ||||
|
| 3 |
即⊙O的半径为2
| 3 |
点评:本题考查了切线的性质、圆周角定理、等边三角形的判定以及锐角三角函数的知识;主要考查学生综合运用定理进行推理和计算的能力.

练习册系列答案
相关题目
(-1)2011+(-1)2010÷|1|+(-1)2009的值等于( )
| A、0 | B、1 | C、-1 | D、2 |
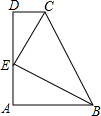 如图,CD∥AB,CE平分∠BCD,BE平分∠ABC,过点E作直线垂直CD于点D,交AB于点A,则下列关系式中成立的有( )
如图,CD∥AB,CE平分∠BCD,BE平分∠ABC,过点E作直线垂直CD于点D,交AB于点A,则下列关系式中成立的有( )①
| CD |
| AD |
| DE |
| AE |
| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |
| A、2个 | B、3个 | C、4个 | D、5个 |
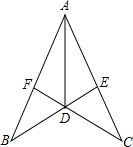 如图,若AB=AC,BE=CF,CF⊥AB,BE⊥AC,则图中全等的三角形共有( )对.
如图,若AB=AC,BE=CF,CF⊥AB,BE⊥AC,则图中全等的三角形共有( )对.| A、5对 | B、4对 | C、3对 | D、2对 |
 如图,在△ABC中,点E在BC边上,点F在AC边的延长线上,AF=BE,连接FE并延长,交AB边于点D,求证:
如图,在△ABC中,点E在BC边上,点F在AC边的延长线上,AF=BE,连接FE并延长,交AB边于点D,求证: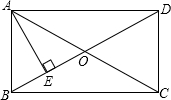 在矩形ABCD中,AD=8cm,对角线比AB边长4cm,则AB=
在矩形ABCD中,AD=8cm,对角线比AB边长4cm,则AB= 如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC= 如图,A,B是⊙O上的两点,∠AOB=120°,C是
如图,A,B是⊙O上的两点,∠AOB=120°,C是