题目内容
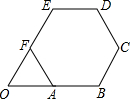 如图,正六边形ABCDEF的边长为2
如图,正六边形ABCDEF的边长为2| 3 |
(1)求直线DF的函数解析式;
(2)求直线DF与直线AE的交点坐标.
考点:正多边形和圆,一次函数图象上点的坐标特征,待定系数法求一次函数解析式
专题:
分析:(1)首先得出△AOF是等边三角形,利用建立的坐标系,得出D,F点坐标,进而求出直线DF的解析式;
(2)由(1)中直线DF的解析式,进而求出横坐标为2时,其纵坐标即可得出答案.
(2)由(1)中直线DF的解析式,进而求出横坐标为2时,其纵坐标即可得出答案.
解答: 解:(1)连接AE,DF,
解:(1)连接AE,DF,
∵正六边形ABCDEF的边长为2
,延长BA,EF交于点O,
∴可得:△AOF是等边三角形,则AO=FO=FA=2
,
∵以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,∠EOA=60°,EO=FO+EF=4
,
∴∠EAO=90°,∠OEA=30°,故AE=4
cos30°=6,
∴F(
,3),D(4
,6),
设直线DF的解析式为:y=kx+b,
则
,
解得:
,
故直线DF的解析式为:y=
x+2,
(2)∵当x=2
时,y=2
×
+2=4,
∴直线DF与直线AE的交点坐标是:(2
,4).
 解:(1)连接AE,DF,
解:(1)连接AE,DF,∵正六边形ABCDEF的边长为2
| 3 |
∴可得:△AOF是等边三角形,则AO=FO=FA=2
| 3 |
∵以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,∠EOA=60°,EO=FO+EF=4
| 3 |
∴∠EAO=90°,∠OEA=30°,故AE=4
| 3 |
∴F(
| 3 |
| 3 |
设直线DF的解析式为:y=kx+b,
则
|
解得:
|
故直线DF的解析式为:y=
| ||
| 3 |
(2)∵当x=2
| 3 |
| 3 |
| ||
| 3 |
∴直线DF与直线AE的交点坐标是:(2
| 3 |
点评:此题主要考查了正多边形和圆以及待定系数法求一次函数解析式等知识,得出F,D点坐标是解题关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
下列各组数中,互为倒数的是( )
| A、2和-2 | ||
B、
| ||
C、2和-
| ||
D、-2和
|
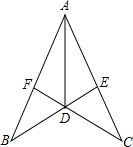 如图,若AB=AC,BE=CF,CF⊥AB,BE⊥AC,则图中全等的三角形共有( )对.
如图,若AB=AC,BE=CF,CF⊥AB,BE⊥AC,则图中全等的三角形共有( )对.| A、5对 | B、4对 | C、3对 | D、2对 |
 如图,在△ABC中,点E在BC边上,点F在AC边的延长线上,AF=BE,连接FE并延长,交AB边于点D,求证:
如图,在△ABC中,点E在BC边上,点F在AC边的延长线上,AF=BE,连接FE并延长,交AB边于点D,求证: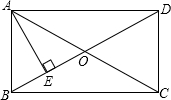 在矩形ABCD中,AD=8cm,对角线比AB边长4cm,则AB=
在矩形ABCD中,AD=8cm,对角线比AB边长4cm,则AB=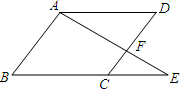 在?ABCD中,延长BC到E,使CE:BC=1:2,连接AE交DC于F,求:S△AFD:S△EFC=
在?ABCD中,延长BC到E,使CE:BC=1:2,连接AE交DC于F,求:S△AFD:S△EFC= 如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC= 如图,AO⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数.
如图,AO⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数. 如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n.
如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n.