题目内容
已知，如图，MN是⊙O的弦，AB是⊙O的直径，AB⊥MN，垂足为点P，半径OC，OD分别交MN于点E，F，且OE=OF．求证：（1）ME=NF．
（2）
 |
| MC |
|
| ND |
考点：垂径定理,圆心角、弧、弦的关系
专题：证明题
分析：（1）先根据垂径定理得出PM=PN，再由OE=OF可知PE=PF，由此可得出结论；
（2）先根据垂径定理得出
=
，再由OE=OF可知OA是线段EF的垂直平分线，故
=
，由此可得出结论．
（2）先根据垂径定理得出
 |
| AM |
|
| AN |
|
| AC |
|
| AD |
解答：证明：（1）∵MN是⊙O的弦，AB是⊙O的直径，AB⊥MN，
∴PM=PN．
∵OE=OF，
∴OA是线段EF的垂直平分线，
∴PE=PF，
∴ME=NF；
（2）∵MN是⊙O的弦，AB是⊙O的直径，AB⊥MN，
∴
=
．
∵OE=OF，
∴OA是线段EF的垂直平分线，
∴
=
，
∴
=
．
∴PM=PN．
∵OE=OF，
∴OA是线段EF的垂直平分线，
∴PE=PF，
∴ME=NF；
（2）∵MN是⊙O的弦，AB是⊙O的直径，AB⊥MN，
∴
|
| AM |
|
| AN |
∵OE=OF，
∴OA是线段EF的垂直平分线，
∴
|
| AC |
|
| AD |
∴
|
| MC |
|
| ND |
点评：本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下面四个实数中，是无理数的为（ ）
| A、0 | ||
B、
| ||
| C、-3 | ||
D、
|
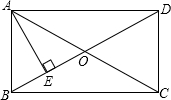在矩形ABCD中，AD=8cm，对角线比AB边长4cm，则AB=
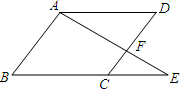在?ABCD中，延长BC到E，使CE：BC=1：2，连接AE交DC于F，求：S△AFD：S△EFC=
如图，在△ABC中，AD是BC上的高，tanB=cos∠DAC，若sinC=若等腰三角形的周长为28cm，一边为11cm，则腰长为（ ）
| A、11cm |
| B、8cm |
| C、11cm或8cm |
| D、以上都不对 |
如图，AO⊥BC于点O，且∠DOC=5∠AOD-12°，求∠BOD的度数．下列各图象中，不能表示y是x的函数的是（ ）
A、 |
B、 |
C、 |
D、 |
用尺规作图：