题目内容
 a、b两数在一条隐去原点的数轴上的位置如图所示,①a-b<0;②a+b<0;③ab<0;④(a+1)(b+1)<0,上述4个式子中一定成立的是
a、b两数在一条隐去原点的数轴上的位置如图所示,①a-b<0;②a+b<0;③ab<0;④(a+1)(b+1)<0,上述4个式子中一定成立的是考点:有理数大小比较,数轴
专题:
分析:根据数轴得出a<-1<b,求出|a|>1>|b|,根据a<b推出a-b<0,根据a<-1<b推出a+1<0,b+1>0,求出(a+1)(b+1)<0,即可得出答案.
解答:解:∵从数轴可知:a<-1<b,
∴|a|>1>|b|,
∴a-b<0,a+b<0,a+1<0,b+1>0,
∴(a+1)(b+1)<0,
∵根据数轴不能确定b的正负,即可ab的符号不能确定,
∴说ab<0错误;
∴①②④正确,
故答案为:①②④.
∴|a|>1>|b|,
∴a-b<0,a+b<0,a+1<0,b+1>0,
∴(a+1)(b+1)<0,
∵根据数轴不能确定b的正负,即可ab的符号不能确定,
∴说ab<0错误;
∴①②④正确,
故答案为:①②④.
点评:本题考查了有理数的大小比较,不等式的基本性质的应用,解此题的关键是能根据a<-1<b推出a+1<0,b+1>0,a-b<0,难度不是很大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 △ABC中,BF、CF是角平分线,∠A=70°,则∠BFC=( )
△ABC中,BF、CF是角平分线,∠A=70°,则∠BFC=( )| A、125° | B、110° |
| C、100° | D、150° |
点P(x,y)在第四象限,P到x轴,y轴的距离分别等于5和3,则P点的坐标是( )
| A、(-3,-5) |
| B、(5,-3) |
| C、(3,-5) |
| D、(-3,5)2 |
 如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC= 如图,A,B是⊙O上的两点,∠AOB=120°,C是
如图,A,B是⊙O上的两点,∠AOB=120°,C是
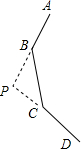 如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n.
如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n. 如图,AB为⊙O的直径,CD为弦,AB=10,CD∥AB,CD=6.
如图,AB为⊙O的直径,CD为弦,AB=10,CD∥AB,CD=6. 用尺规作图:
用尺规作图: