题目内容
菜贩以2.00元/千克的进价购入50千克西红柿,其中有5千克西红柿被挤压或碰撞后,只能按1.80元/千克售出,其余的西红柿有大有小,菜贩准备将之分开出售,大的售价3.00元/千克,小的售价2.50元/千克,
(1)西红柿全部售完后,平均每千克至多净赚多少元?至少净赚多少元?
(2)如果希望西红柿全部售完后每千克净赚0.6元,那么至少应有多少千克的西红柿售价是3.00.
(1)西红柿全部售完后,平均每千克至多净赚多少元?至少净赚多少元?
(2)如果希望西红柿全部售完后每千克净赚0.6元,那么至少应有多少千克的西红柿售价是3.00.
考点:一元一次不等式的应用
专题:
分析:(1)利用已知求出成本,进而利用销售最大值以及最小值求出总利润,进而得出平均价格;
(2)根据希望西红柿全部售完后每千克净赚0.6元,表示出总利润得出等式,进而得出答案.
(2)根据希望西红柿全部售完后每千克净赚0.6元,表示出总利润得出等式,进而得出答案.
解答:解:(1)总投入:50×2=100(元)
要达到最大利润,则好的全部卖3元每斤.
则有:3×(50-5)+1.8×5=144(元),
故最多净赚144-100=44(元),
最多每千克获利:44÷50=0.88(元);
若利润最小,则好的全部卖2.5元每斤.
则有:2.5×(50-5)+1.8×5=121.5(元),
故至少净赚121.5-100=21.5(元),
最少每千克获利:21.5÷50=0.43(元),
答:平均每千克至多净赚0.88元,至少净赚0.43元;
(2)设卖3.00元一斤的为x斤,则有:
3x+2.5(50-5-x)+5×1.8-100≥0.6×50
解得:x≥17,
答:至少要卖17千克3.00元每斤的西红柿,才能至少每斤净赚0.6元每斤.
要达到最大利润,则好的全部卖3元每斤.
则有:3×(50-5)+1.8×5=144(元),
故最多净赚144-100=44(元),
最多每千克获利:44÷50=0.88(元);
若利润最小,则好的全部卖2.5元每斤.
则有:2.5×(50-5)+1.8×5=121.5(元),
故至少净赚121.5-100=21.5(元),
最少每千克获利:21.5÷50=0.43(元),
答:平均每千克至多净赚0.88元,至少净赚0.43元;
(2)设卖3.00元一斤的为x斤,则有:
3x+2.5(50-5-x)+5×1.8-100≥0.6×50
解得:x≥17,
答:至少要卖17千克3.00元每斤的西红柿,才能至少每斤净赚0.6元每斤.
点评:此题主要考查了一元一次不等式的应用,根据题意结合利润得出正确的等量关系是解题关键.

练习册系列答案
相关题目

 如图,已知△ABC的内切圆O切AC于点K,D是AC的中点,求证:直线DO平分线段BK.
如图,已知△ABC的内切圆O切AC于点K,D是AC的中点,求证:直线DO平分线段BK. 如图,直线l1:y=ax+2与y轴相交于点E,已知A(-2,1),B(-2,-1),C(1,-1)且ABCD是矩形,设l2过点E,且l1⊥l2,
如图,直线l1:y=ax+2与y轴相交于点E,已知A(-2,1),B(-2,-1),C(1,-1)且ABCD是矩形,设l2过点E,且l1⊥l2,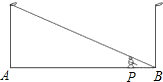 如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为
如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为